Экстремальные свойства главных напряжений.
Возьмем в теле произвольную точку А (х, у, z). Через эту точку можно провести бесконечное множество площадок. Очевидно, что на одной из площадок нормальное напряжение достигнет наибольшего для данной точки значения, а на другой касательное напряжение примет свое максимальное значение.
Пусть для точки А известно положение главных осей напряженного состояния. Если их принять за систему координат (рис.23), то в наклонной площадке с вектором нормали n (l, m, n) возникают нормальные и касательные напряжения Р(s, t). Определим эти напряжения и исследуем их экстремальные свойства.
 |
Рис. 23
Нормальные напряжения в любой наклонной площадке выражаются основной квадратичной формой (33). Запишем её с учетом того, что в качестве системы координат приняты главные оси:
sn = s1×l2 + s2×m2 + s3×n2. (38)
Найдем квадрат полного напряжения на наклонной площадке как сумму квадратов его проекций, выражения для которых были найдены ранее (32):
Р2 = Pх2+ Pу2 + Pz2 = s12×l2 + s22×m2 + s32×n2 . (39)
Также полное напряжение на наклонной площадке можно представить как сумму нормального и касательного напряжений (17).
Таким образом, мы имеем систему трех уравнений с тремя неизвестными - l2, m2, n2:
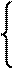 s = s1×l2 + s2×m2 + s3×n2,
s = s1×l2 + s2×m2 + s3×n2,
s2 + t2 = s12×l2 + s22×m2 + s32×n2, (40)
1 = l2 + m2 + n2 .
Умножим каждое уравнение на произвольные множители a, b, c и сложим, сгруппировав при этом слагаемые по направляющим косинусам
а×s + b×(s2 + t2) + с =
= l2×(а×s1 + b×s12 + с) + m 2×(а×s2 + b×s22 + с) + n 2×(а×s3 + b×s32 + с). (41)
Для определения величины l2 подберем коэффициенты a, b, c таким образом, чтобы вторая и третья скобки в правой части уравнения (41) обнулились:
а×s2 + b×s22 + с = 0,
а×s3 + b×s32 + с = 0,
получаем
b = 1, а = -(s2 +s3), с = s2×s3.
Подставляя полученные коэффициенты в уравнение (41), находим величину l2:
l2=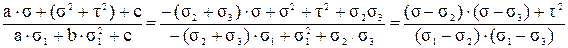 . (42)
. (42)
Аналогично находим квадраты двух других направляющих косинусов
m 2 = 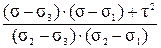 ,
,
(43)
n 2 = 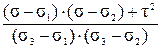 .
.
В уравнениях (42) и (43) дроби должны быть больше нуля, так как в левых частях стоят квадраты величин. Проанализируем знаменатели дробей на основе неравенства s1 ³ s2 ³ s3:
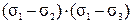 ³ 0,
³ 0,
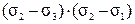 £ 0, (44)
£ 0, (44)
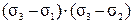 ³ 0.
³ 0.
На основе неравенств (44) можно сделать вывод о знаке числителя:
 |
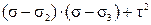 ³ 0,
³ 0,
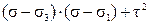 £ 0, (45)
£ 0, (45)
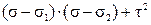 ³ 0.
³ 0.
Сделав ряд математических преобразований, можно показать, что неравенства (45) представляют собой области, ограниченные окружностями. Рассмотрим третье неравенство и представим его решение графически (рис.24):
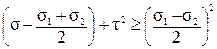 . (46)
. (46)
Представим решение системы (45) графически (рис. 25). Эта диаграмма называется круговой диаграммой Мора. Круговая диаграмма позволяет установить экстремальные свойства нормальных и касательных напряжений.
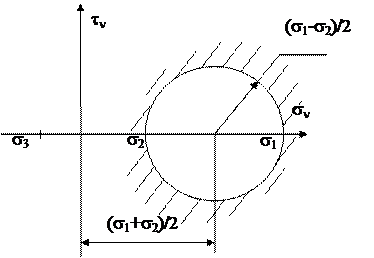 |
Рис. 24
s1 - максимальное нормальное напряжение, которое может возникнуть в точке на любой наклонной площадке;
s3 - минимальное нормальное напряжение, которое может возникнуть в точке на любой наклонной площадке;
tmax = 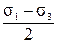 - максимальное касательное напряжение, которое может возникнуть в точке на любой наклонной площадке, действует на площадках наклоненных к главным на угол 45°.
- максимальное касательное напряжение, которое может возникнуть в точке на любой наклонной площадке, действует на площадках наклоненных к главным на угол 45°.
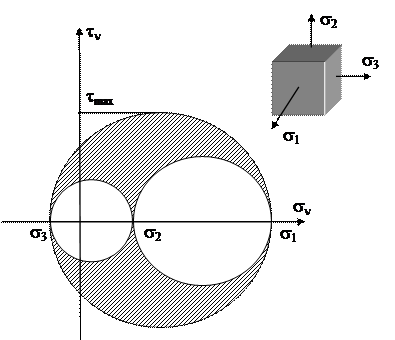 |
Рис. 25
 2014-02-03
2014-02-03 3231
3231








