2014-02-03
554
Рис.115
Рис.114
По теореме об изменении количества движения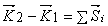 
в проекциях на оси х и у получим два уравнения:
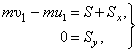
где скорости центра масс С в начале и конце удара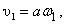 
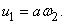Поэтому первое уравнение станет таким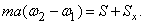 
Третье уравнение, по (10), получится в виде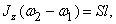 
из которого находим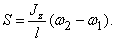 
И, так как коэффициент восстановления
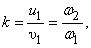
то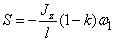 
(в нашем примере 
поэтому ударный импульс S > 0, то есть направлен так, как показано на рисунке).
Находим импульсы реакции оси: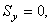 
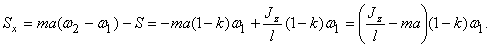
Обязательно надо обратить внимание на то, что при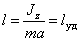 
ударные импульсы в подшипниках оси будут равны нулю.
Место, точка удара, расположенная на этом расстоянии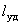 
от оси вращения, называется центром удара. При ударе по телу в этом месте ударные силы в подшипниках не возникают.
Кстати, заметим, что центр удара совпадает с точкой где приложены равнодействующая сил инерции и вектор количества движения.
Вспомним, что при ударе длинной палкой по неподвижному предмету, мы нередко испытывали рукой неприятный ударный импульс, как говорят – «отбивали руку».
Нетрудно найти в этом случае центр удара – место, которым следует ударить, чтобы не почувствовать это неприятное ощущение (рис.115).
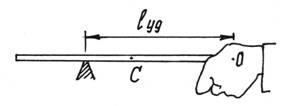
Так как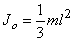 
(l – длина палки) и 
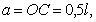то
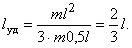
Следовательно, центр удара находится на расстоянии трети длины от конца палки.
Понятие центра удара учитывают при создании различных ударных механизмов и других конструкций, где встречаются ударные процессы.
В данной лекции рассматриваются следующие вопросы:
- Динамика точки.
- Основные понятия и определения.
- Законы динамики.
- Задачи динамики для свободной и несвободной материальной точки.
- Дифференциальные уравнения движения точи.
- План решения второй задачи движения.
- Движение точки, брошенной под углом к горизонту в однородном поле тяжести.
- Относительное движение материальной точки.
- Влияние вращения Земли на равновесие и движение тел.
- Общие теоремы динамики точки.
- Количество движения.
- Импульс силы.
- Теорема об изменении количества движения точки.
