Асимптотойкривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой (рис. 16).
Асимптоты могут быть вертикальными, наклонными и горизонтальными.
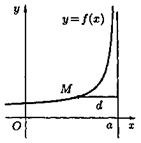
Рис. 16.
Говорят, что прямая х = а является вертикальной асимптотойграфика функции у = f (x),если 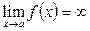 или
или 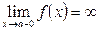 , или
, или 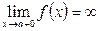 .
.
Действительно, в этом случае непосредственно из рисунка 16 видно, что расстояние точки М (х; у)кривой от прямой х = а равно d = |х - а|. Если х → а, то d → 0. Согласно определению асимптоты, прямая х = а является асимптотой кривой у = f (x). Для отыскания вертикальных асимптот нужно найти те значения х,вблизи которых функция f (x)неограниченно возрастает по модулю. Обычно это точки разрыва второго рода.
Уравнение наклонной асимптотыбудем искать в виде
y = kx + b. (11.5)
Найдем k и b.
Пусть М (х; у)- произвольная точка кривой у = f (x)
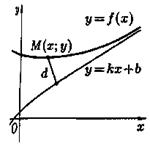 (см. рис. 17). По формуле расстояния от точки до
(см. рис. 17). По формуле расстояния от точки до
прямой 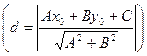 находим расстояние от
находим расстояние от
точки М до прямой (11.5): 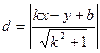 .
.
Рис.17
Условие d → 0 будет выполняться лишь тогда, когда числитель дроби стремится к нулю, т. е.
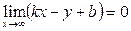 (11.6)
(11.6)
Отсюда следует, что kx - у + b = α, где α= α(х) бесконечно малая: α →0 при х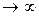 . Разделив обе части равенства у = b + kx - α на х и перейдя к пределу при х
. Разделив обе части равенства у = b + kx - α на х и перейдя к пределу при х 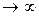 , получаем:
, получаем: 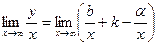 .
.
Так как 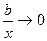 и
и 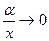 ,
,
то 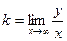 . (11.7)
. (11.7)
Из условия (11.6) находим b:
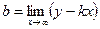 (11.8)
(11.8)
Итак,если существует наклонная асимптота у = kx + b, то k и b находятся по формулам (11.7) и (11.8).
Верно и обратное утверждение: если существуют конечные пределы (11.7) и (11.8), то прямая (11.5) является наклонной асимптотой.
Если хотя бы один из пределов (11.7) или (11.8) не существует или равен бесконечности, то кривая у = f (x) наклонной асимптоты не имеет.
В частности, если k = 0, то 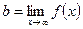 . Поэтому у = b - уравнение
. Поэтому у = b - уравнение
горизонтальной асимптоты.
Замечание: Асимптоты графика функции у = f (x)при х 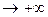 и х
и х 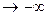 могут быть разными. Поэтому при нахождении пределов (11.7) и (11.8) следует отдельно рассматривать случай, когда х
могут быть разными. Поэтому при нахождении пределов (11.7) и (11.8) следует отдельно рассматривать случай, когда х 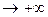 и когда х
и когда х 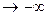 .
.
 2014-02-03
2014-02-03 1537
1537







