Теорема (Правило Лопиталя раскрытия неопределенностей вида 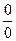 ).
).
Пусть функции f (х) и φ (x) непрерывны и дифференцируемы в окрестности точки x 0и обращаются в нуль в этой точке: f (x 0) = φ (x 0) = 0. Пусть φ '(х) ≠ 0 в окрестности точки x 0. Если существует предел 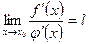 , то
, то 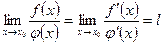 .
.
Замечания:
1. Теорема верна и в случае, когда функции f (x) и φ (х) не определены при х = x 0, но 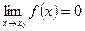 и
и 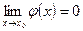 . Достаточно положить
. Достаточно положить
f (x 0) = 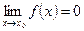 и φ (x 0) =
и φ (x 0) = 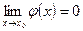
2. Теорема справедлива и в том случае, когда х →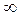 . Действительно,
. Действительно,
положив x = 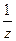 , получим
, получим 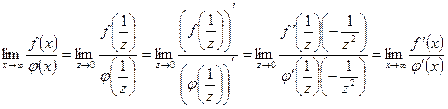 .
.
3. Если производные f '(x) и φ '(x) удовлетворяют тем же условиям, что и функции f (x) и φ (x), теорему можно применить еще раз: 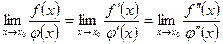 и т. д.
и т. д.
Теорема. (Правило Лопиталя раскрытия неопределенностей вида 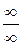 ).
).
Пусть функции f (x) и φ (х) непрерывны и дифференцируемы в окрестности точки x 0 (кроме, может быть, точки x 0), в этой окрестности 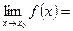
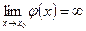 , φ ′(x) ≠ 0. Если существует предел
, φ ′(x) ≠ 0. Если существует предел 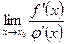 , то
, то 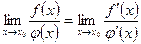 .
.
 2014-02-03
2014-02-03 1090
1090
