Дифракция сферических волн

Дифракция сферических волн (дифракция Френеля) - дифракци­онная картина наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию. Обычно рассчитывается графически.

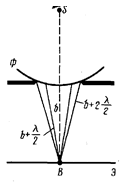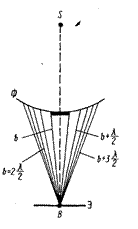
1. Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием радиуса 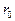. Дифракционную картину наблюдаем на экране (Э) в точке В, лежащей на линии, соединяющей S с центром отверстия. b- расстояние от вершины волновой поверхности до т. В, а- радиус волновой поверхности.

Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, укладывающихся в отверстии:.

¨ в отсутствие непрозрачного экрана с отверстием в т. В амплитуда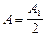

¨ в отверстие уклады­вается нечетное число m зон Френеля,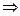в т. В амплитуда 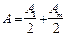больше, чем в отсутствие непрозрачного экрана. Напр., если в отверстие уклады­вается одна зона Френеля, 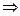в т. В амплитуда А=А₁, вдвое больше, чем в отсутствие непрозрачного экрана (интенсивность света больше в четыре ра­за) – наблюдается максимум.

¨ в отверстие уклады­вается четное число m зон Френеля, 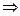в т. В амплитуда 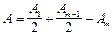меньше, чем в отсутствие непрозрачного экрана. Напр., в отверстии укладываются две зоны Френеля, 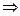в т. В амплитуда 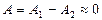(волны практически уничтожат друг друга из-за интерференции) – наблюдается минимум.

1) Дифрак­ционная картина от круглого отверстия вблизи точки В будет иметь вид чередую­щихся темных и светлых колец с центрами в точке В (если m четное, то в центре будет темное кольцо, если т нечетное — то светлое кольцо), причем интенсивность максимумов убывает с расстоянием от центра картины.

2) Если отверстие освещается не монохроматическим, а бе­лым светом, то кольца окрашены.

3) Число зон Френеля, укладывающихся в отверстии. Есл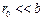и и 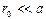и радиус удовлетворяет условию (12.3), то отверстие оставит открытым 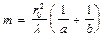(13.1)

4) Если диаметр отверстия велик 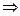- интерференционной картины не будет – свет будет распространяться почти так же, как в отсутствии экрана – прямолинейно, (точнее: чередование темных и светлых колец наблюдается лишь в очень узкой области на границе геометрической тени; внутри этой области освещенность оказывается практически постоянной).

Замечание: Расчет произведен для точки, лежащей против центра отверстия. Расчет амплитуды результирующих колебаний в других точках участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непрозрачным экраном.

Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально при помощи зонных пластинок – стеклянных пластинок, состоящих из системы чередующихся прозрачных и непрозрачных колец, построенных по принципу расположения зон Френеля.

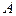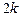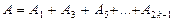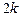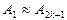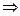Величину можно сделать очень большой при помощи зонной пластинки, в которой непрозрачное покрытие закрывает все четные зоны Френеля и оставляет открытыми все нечетные зоны. Если общее число зон, умещающихся на пластинке, равно , то . Если не слишком велико, то и освещенность экрана в т. В в 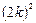раз больше, чем при беспрепятственном распространении света от источника в т. В.

2. Дифракция на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционную картину наблюдаем на экране (Э) в точке В, лежащей на линии, соединяющей S с центром диска. Закрытый диском участок фронта волны надо исклю­чить из рассмотрения и зоны Френеля строить начиная с краев диска. Пусть диск закрывает т первых зон Френеля.

1. В точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствую­щий половине действия первой открытой зоны Френеля .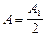

2. Центральный максимум ок­ружен концентрическими темными и светлыми кольцами, а интенсивность максимумов убывает с расстоянием от центра картины. С увеличением радиуса диска первая открытая зона Френеля удаляется от т. S и увеличивается угол 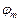между нормалью к поверхности этой зоны и направлением на т. В.

3. С увеличением размеров диска интенсивность центрального мак­симума уменьшается.

4. При больших размерах диска за ним наблюдается тень, вблизи границ которой имеет место слабая дифракционная картина - свет распространяющимся почти пря­молинейно.

Замечание: Если форма краев экранов и отверстий в них от­личается от геометрически идеальной, то дифракционные закономерности не выполняются. Степень отклонения от этих закономерностей определяется вели­чиной 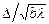, где 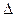—длина основания или высота вы­ступов (шероховатостей) на краях экрана, b— расстоя­ние от экрана до точки наблюдения, 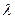—длина волны:

а) 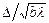< 1 — нарушения дифракционной картины практически отсутствуют;

б) 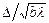~1—дифракционная картина сглаживается и может исчезнуть;

в) 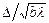>1—дифракционные полосы или кольца по­вторяют конфигурацию выступов и впадин на внешних краях экранов или краях отверстий в них.

14. Дифракция плоских све­товых волн

Дифракция плоских све­товых волн (дифракция в параллель­ных лучах) - источник света и точка наблюдения бесконечно уда­лены от препятствия, вызвавшего диф­ракцию.

Дифракция света наблюдается на:

1) плоской одномерной решетке (штрихи нанесены перпендикулярно некоторой пря­мой линии);

2) двумерной решетке (штрихи нанесены во взаимно перпендику­лярных направлениях в одной и той же плоскости);

3) пространственных (трехмерных) решетках — пространствен­ных образованиях, в которых элементы структуры подобны по форме, имеют гео­метрически правильное и периодически по­вторяющееся расположение, а также по­стоянные (периоды) решеток, соизмери­мые с длиной волны электромагнитного излучения, подобные про­странственные образования должны иметь периодичность по трем не лежащим в одной плоскости направлениям. В качестве пространственных дифракционных реше­ток могут быть использованы кристалли­ческие тела, так как в них неоднородности (атомы, молекулы, ионы) регулярно по­вторяются в трех направлениях.

Замечания:

1. Для наблюдения дифракционной картины необходимо, чтобы постоянная решетки была того же порядка, что и длина волны падающего излучения.

2. Световые волны будем считать плоскими монохроматическими.

3. При расчете дифракционной картины на щели и одномерной решетке считается, что свет падает нормально.

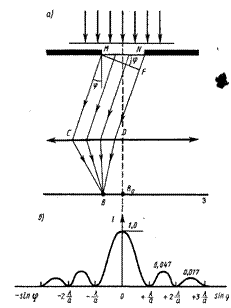1. Дифракция Фраунгофера на бесконечно длинной щели. Чтобы этот тип дифракции осу­ществить, надо а) точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину иссле­довать в фокальной плоскости второй со­бирающей линзы, установленной за пре­пятствием или б) чтобы длина ще­ли была значительно больше ее ширины. При визуальном наблюдении вместо линзы и экрана пользуются зрительной трубой, настроенной на бесконечность. Этот вид дифракции обычно рассчитывается аналитически.

Пусть плоская монохроматическая свето­вая волна падает нормально плоскости узкой щели шириной а. Опти­ческая разность хода между крайними лучами МС и ND, идущими от щели в про­извольном направлении,

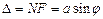, (14.1)

где F — основание перпендикуляра, опу­щенного из точки М на луч ND,

Разобьем открытую часть волновой по­верхности в плоскости щели MN на зоны Френеля, имеющие вид полос, параллель­ных ребру М щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна , т. е. всего на ширине щели уместится 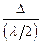зон. Так как свет на щель падает нормально, то плоскость щели совпадает с фронтом волны; следовательно, все точки фронта в плоскости щели будут колебаться в оди­наковой фазе. Амплитуды вторичных волн в плоскости щели будут равны, так как выбранные зоны Френеля имеют оди­наковые площади и одинаково наклонены к направлению наблюдения.

Следствие

1. число зон Френеля, укладывающихся на ширине щели, зависит от угла .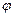

2. при интерференции света от каждой пары соседних зон Френеля амплитуда резуль­тирующих колебаний равна нулю (колебания от каждой пары соседних зон взаимно погашают друг друга).

Если число зон Френеля четное, то в точке В наблюдается дифракционный минимум (полная темнота): 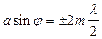(m=1, 2, 3,...), (14.2)

если число зон Френеля нечетное, то наблюдается дифракционный макси­мум, соответствующий действию одной нескомпенсированной зоны Френеля

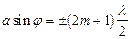(m=1, 2, 3,...), (14.3)

В прямом направлении (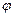=0) щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсивностью - в точке В₀ наблюдается центральный дифракционный максимум.

Из 14.2 и 14.3 можно найти направления на точки экрана, в ко­торых амплитуда (ин­тенсивность) равна нулю или максимальна.

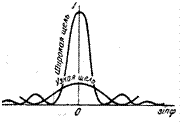
Опр. 14.1 Дифракционный спектр - распределение ин­тенсивности на экране, получаемое вслед­ствие дифракции (приведено на рисунке).

Интенсивность постепенно спа­дает от центра в плоскости наблюдения к ее краям (интенсивности централь­ного и последующих максимумов относят­ся как 1: 0,047: 0,017: 0,0083:...,)т. е. основ­ная часть световой энергии сосредоточена в центральном максимуме. Су­жение щели - максимумы (цен­тральный и др.) интенсивности расширяются и уменьшают­ся в высоте (расплываются), а их яркость уменьшается.

При - минимумы вообще не возникают, интенсивность света монотонно убывает от середины к ее краям.

При а=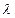 первый минимум уходит в бесконечность

Чем щель шире (а>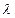), тем карти­на ярче, дифракционные полосы уже, число полос больше.

При a>>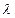 в центре получается резкое (геометрическое) изображение щели без признаков дифракционной картины, т. е. имеет место прямо­линейное распространение света.

Угловая ширина центрального максимума 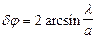(14.4)

При a>>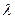 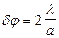(14.4’)

Положение дифракционных максиму­мов зависит от длины волны 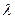, поэтому рассмотренный вид дифракционная карти­на имеет лишь для монохроматического света. При освещении щели белым светом центральный максимум имеет вид белой полоски; он общий для всех длин волн (при 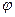=0 разность хода равна нулю для всех 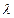). Боковые максимумы радужно ок­рашены, так как условие максимума при любых т различно для разных 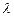. Справа и слева от центрального максимума наблюдаются максимумы пер­вого (m=1), второго (m=2) и других порядков, обращенные фиолетовым краем к центру дифракционной картины. Однако они настолько расплывчаты, что отчетли­вого разделения различных длин волн с помощью дифракции на одной щели получить невозможно.