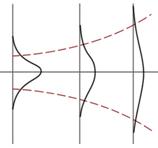
У гауссовского пучка амплитуда из центра к периферии меняется по закону Гаусса. (в любой плоскости, перпендикулярной оптической оси)
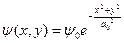
Данная функция обладает свойством: при использовании преобразования Френеля 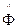 или Фурье
или Фурье 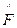 она преобразуется в подобную же ей.
она преобразуется в подобную же ей.
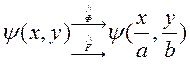 (подобные функции, распределение поля то же, но растянуто в плоскости.)
(подобные функции, распределение поля то же, но растянуто в плоскости.)
Этим свойством обладает не только пучки с Гауссовым распределением, но и Гауссо-Эрмитовы пучки (пучки высшего порядка).
1. 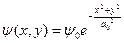
Координаты в окне - (x,y), координаты точки А – (x’,y’)
Введем переобозначения: (x,y)=>(ξ, η); (x’,y’)=>(x,y)
Преобразование Френеля:
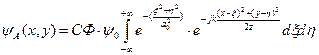
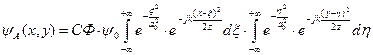 =
=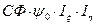
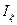 можно свести к табличному интегралу Пуассона
можно свести к табличному интегралу Пуассона 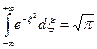 путем замены переменных. Выделим в показателе экспоненты: (
путем замены переменных. Выделим в показателе экспоненты: (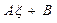 )=
)= 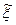 (
(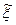 -новая переменная), домножим/разделим на
-новая переменная), домножим/разделим на 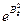
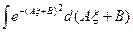 =
=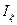 =
=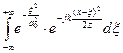 =
=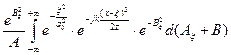
Сравнивая коэффициенты при степенях ξ:
| ξ2 | -А2 | -1/а02-jk/2z |
| ξ | -2AB | jkx/z |
Отсюда A=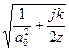 и Bξ=
и Bξ=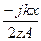 . Аналогичные вычисления проводятся и для
. Аналогичные вычисления проводятся и для 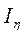
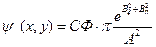
Можно показать, что воспользовавшись выражением для A и В, получается значение поля:
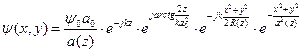
где 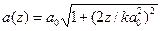 и
и 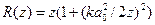
Т.е.
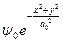 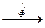 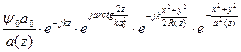 |
 2014-02-03
2014-02-03 1271
1271








