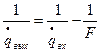Таблица сравнения гауссова и гомоцентрического пучков.
| Гомоцентрический пучок | Гауссов пучок | ||
| 1. Прохождение слоя пространства | |||
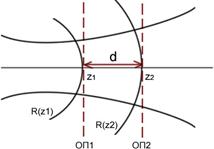
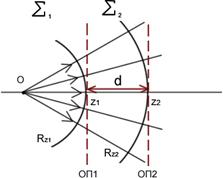 Rz1-радиус кривизны ОП1,ОП2 –опорные плоскости 1 и 2 d=z2-z1 –слой пространства Rz1-радиус кривизны ОП1,ОП2 –опорные плоскости 1 и 2 d=z2-z1 –слой пространства
|  OП1: OП1: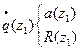 , ОП2: , ОП2: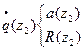 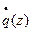 = =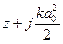 , ,
При прохождении слоя пространства комплексный параметр преобразуется как радиус кривизны волнового фронта гомоцентрического пучка. | ||
| 2. Прохождение пучка через тонкую линзу | |||
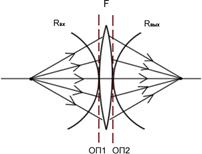 Rвх, Rвых -радиусы кривизны волнового фронта. Связь между ними определяется формулой тонкой линзы. Формула тонкой линзы на языке радиуса кривизны волнового фронта: Rвх, Rвых -радиусы кривизны волнового фронта. Связь между ними определяется формулой тонкой линзы. Формула тонкой линзы на языке радиуса кривизны волнового фронта:
где Т.о. кривизна волнового фронта на выходе равна кривизне волнового фронта на входе минус оптическая сила. | 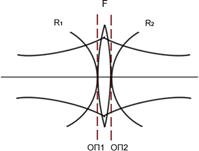 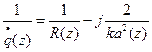 a2(z) = a1(z) Вещественная часть, отвечающая за кривизну изменяется по формуле тонкой линзы для кривизны: a2(z) = a1(z) Вещественная часть, отвечающая за кривизну изменяется по формуле тонкой линзы для кривизны:
|
Радиус кривизны волнового фронта гомоцентрического пучка и комплексный параметр Гауссова пучка 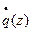 преобразуются одинаковым образом при прохождении слоя пространства и тонкой линзы. Поэтому можно пользоваться существующей аналогией.
преобразуются одинаковым образом при прохождении слоя пространства и тонкой линзы. Поэтому можно пользоваться существующей аналогией.
Пример:
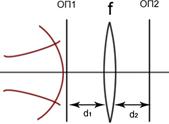
1) ОП1: Rвх, авх, 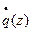
2) На входе линзы 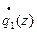 =
=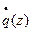 +d1
+d1
3) Прохождение тонкой линзы: 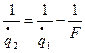
4) ОП2: 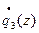 =
=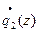 +d2
+d2
Для упрощения процедуры расчета Гауссовых пучков можно воспользоваться представлением о лучевых матрицах: (приводятся, опираясь на аналогию между радиусом кривизны гомоцентрического пучка и комплексным параметром Гауссова пучка)
Для гомоцентрического пучка
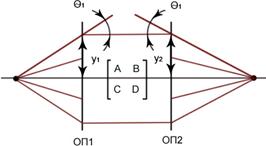
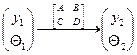 ,
, 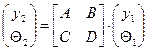 ,
, 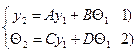 ,
,
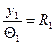 -радиус кривизны на входе,
-радиус кривизны на входе, 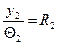 -радиус кривизны на выходе.
-радиус кривизны на выходе.
разделим 1 на 2, 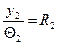 =
=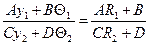
В силу существующей аналогией между R и 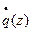 :
:
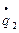 = =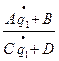 |
-Теорема ABCD для Гауссовых пучков.
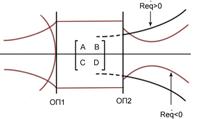
Комплексным параметром Гауссова пучка 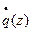 =
=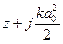 .
.
Перетяжка: Re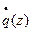 =z, a0=
=z, a0=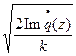
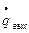 =
=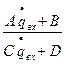
При использовании лучевых матриц при расчете гауссовых пучков следует обратить внимание на другие матрицы:
 | 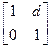 (матрица слоя пространства) (матрица слоя пространства) |
 | 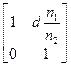 |
 | 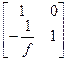 |
Пример1 «d1-f-d2»
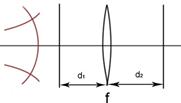
d1=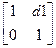 , f=
, f=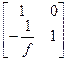 , d2=
, d2=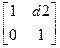
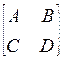 =
=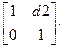
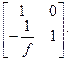
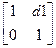 =
=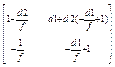
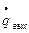 =
=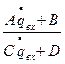 =
=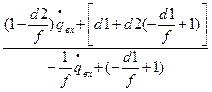
Пример2 Задача о преобразовании Гауссова пучка в пучок с заданными параметрами.
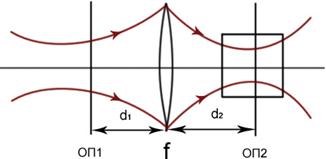
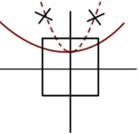
ОП1: 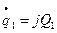 , ОП2
, ОП2 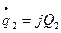
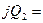
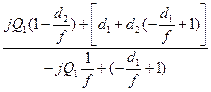
Надо определить: d1, d2, f
Из данного уравнения можно получить 2 выражение для Re и Im частей:
Re: 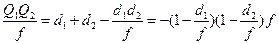
Im: 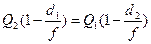
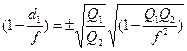
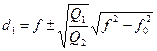 | 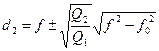 |
Пример3 Рассмотрим вопрос по передаче гауссова пучка в линзовом волноводе.
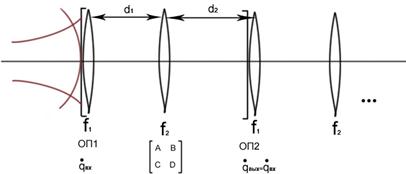
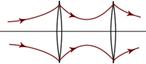
Система устойчива, если в ОП2 будет qвых = qвх (qвх в ОП1)
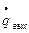 =
=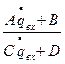 , замена q= qвых =qвх,
, замена q= qвых =qвх, 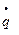 =
=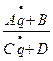 ,
, 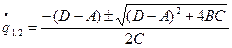
Т.к. рассматриваемая среда везде имеет один показатель преломления n: det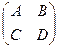 =1=AD-BC
=1=AD-BC
Приведем выражение для 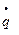 к форме, содержащей действительную и мнимую части.
к форме, содержащей действительную и мнимую части.
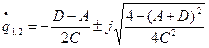 , но
, но 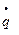 =z+jQ, следовательно выбираем решение со знаком +, т.е.:
=z+jQ, следовательно выбираем решение со знаком +, т.е.:
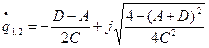 |
Полученное выражение определяет 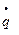 -параметр гауссова пучка, который будет согласован с линзовым волноводом (т.е. устойчиво передаваться по линзовому волноводу)
-параметр гауссова пучка, который будет согласован с линзовым волноводом (т.е. устойчиво передаваться по линзовому волноводу)
Но решение будет не при любых 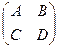 , оно существует только при условии, что подкоренное выражение
, оно существует только при условии, что подкоренное выражение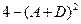 было больше нуля, т.е:
было больше нуля, т.е:
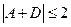 |
-условие устойчивости лазерного волновода.
//----------------------------------------------------------------------------------------------------------------------
 2014-02-03
2014-02-03 3306
3306

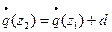
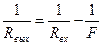
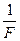 -оптическая сила.
-оптическая сила.