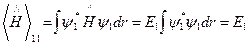 , ,
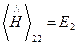 , ,
| 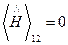 , ,
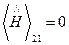 , ,
|
4. Эрмитовы операторы:
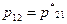 ,
, 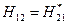
5. Принцип суперпозиции:

| Система описывается:

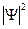 -плотность вероятности -плотность вероятности
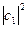 и и 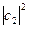 -вероятности обнаружить систему в состоянии 1 и 2 соответственно. -вероятности обнаружить систему в состоянии 1 и 2 соответственно.
|
6. Значение дипольного момента:
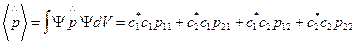 , но
, но 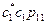 =0,
=0, 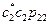 =0, следовательно:
=0, следовательно:
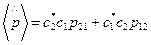 , где
, где 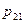 и
и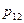 -матричные элементы.
-матричные элементы.
Если состояние определяется (состояний может быть много):
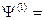
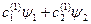
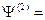
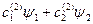
…
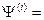
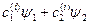
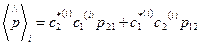
Среднее по i состояниям:
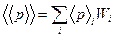 , где
, где 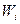 - вероятность i-го состояния.
- вероятность i-го состояния.
Выражение 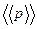 -величина, которая содержит 2 усреднения: по квантово-механическому состоянию и по ансамблю (i)
-величина, которая содержит 2 усреднения: по квантово-механическому состоянию и по ансамблю (i)
Получаем:
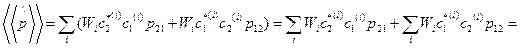
=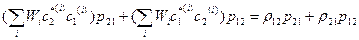
ρ- учитывает не только квантово-механическое, но и термодинамическое состояние системы.
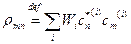 -матрица плотности. Она описывает ансамбль микрочастиц.
-матрица плотности. Она описывает ансамбль микрочастиц.
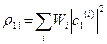 -вероятность того, что любая частица находится в 1 состоянии в ансамбле. (
-вероятность того, что любая частица находится в 1 состоянии в ансамбле. (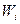 -вероятность, что можно получить i-е состояние,
-вероятность, что можно получить i-е состояние, 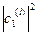 - вероятность обнаружения 1 частицу в 1 квантовом состоянии)
- вероятность обнаружения 1 частицу в 1 квантовом состоянии)
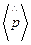 - квантово-механическое среднее
- квантово-механическое среднее
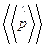 - усреднение по ансамблю
- усреднение по ансамблю
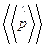
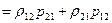 - след матрицы (spur)
- след матрицы (spur) 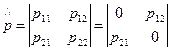
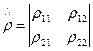 ,
, 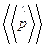
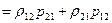 =
=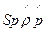
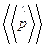 = =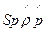
|
 2014-02-03
2014-02-03 358
358








