2014-02-03
476
Лекция № 21.
Несобственные интегралы.
Пусть функция f(x) определена и непрерывна на интервале [a, ¥). Тогда она непрерывна на любом отрезке [a, b].
Определение: Если существует конечный предел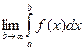 
, то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥).
Обозначение: 
Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится.
Если предел не существует или бесконечен, то несобственный интеграл расходится.
Аналогичные рассуждения можно привести для несобственных интегралов вида:
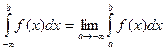
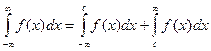
Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.
Пример.
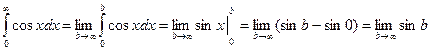- не существует.
Несобственный интеграл расходится.
Пример.
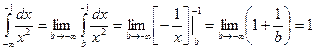- интеграл сходится
Теорема: Если для всех х (x ³ a) выполняется условие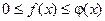 
и интеграл 
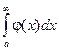сходится, то 
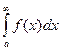тоже сходится и 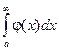³ .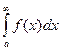
Теорема: Если для всех х (x ³ a) выполняется условие 
и интеграл 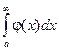расходится, то 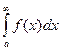тоже расходится.
Теорема: Если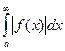 
сходится, то сходится и интеграл .
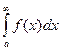В этом случае интеграл 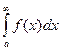называется абсолютно сходящимся.
|
|
|
Интеграл от разрывной функции.
Если в точке х = с функция либо неопределена, либо разрывна, то
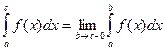
Если интеграл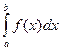 
существует, то интеграл 
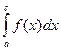- сходится, если интеграл 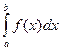не существует, то 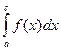- расходится.
Если в точке х = а функция терпит разрыв, то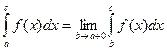 
.
Если функция f(x) имеет разрыв в точке b на промежутке [a, с], то
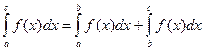
Таких точек внутри отрезка может быть несколько.
Если сходятся все интегралы, входящие в сумму, то сходится и суммарный интеграл.
