Формулы интегрирования при помощи замены переменной для неопределенного интеграла.
Лекция № 18.
Способ подстановки (замены переменных).
Теорема: Если требуется найти интеграл 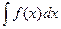 , но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
, но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
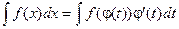
Доказательство: Продифференцируем предлагаемое равенство:
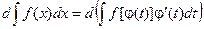
По рассмотренному выше свойству №2 неопределенного интеграла:
f(x)dx = f[j(t)]j¢(t)dt
что с учетом введенных обозначений и является исходным предположением. Теорема доказана.
Пример. Найти неопределенный интеграл 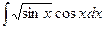 .
.
Сделаем замену t = sinx, dt = cosxdt.
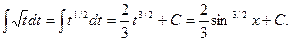
Пример. 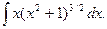
Замена 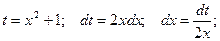 Получаем:
Получаем:
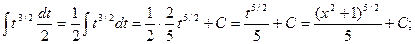
Ниже будут рассмотрены другие примеры применения метода подстановки для различных типов функций.
Интегрирование по частям.
Способ основан на известной формуле производной произведения:
(uv)¢ = u¢v + v¢u
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем: 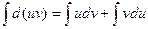 , а в соответствии с приведенными выше свойствами неопределенного интеграла:
, а в соответствии с приведенными выше свойствами неопределенного интеграла:
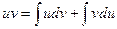 или
или 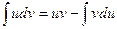 ;
;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Пример. 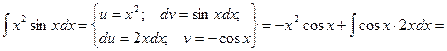
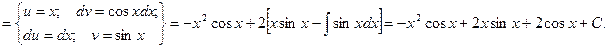
Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.
Пример. 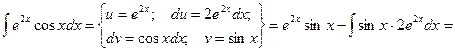
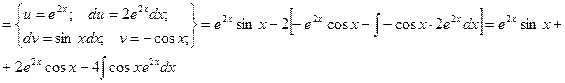
Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.
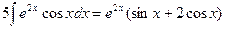
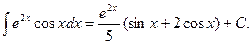
Таким образом, интеграл найден вообще без применения таблиц интегралов.
Прежде чем рассмотреть подробно методы интегрирования различных классов функций, приведем еще несколько примеров нахождения неопределенных интегралов приведением их к табличным.
Пример.
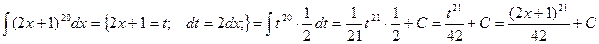
Пример.
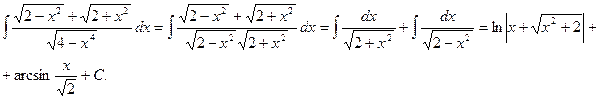
Пример.
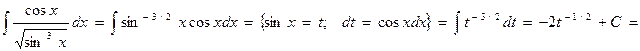
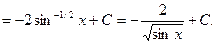
Пример.
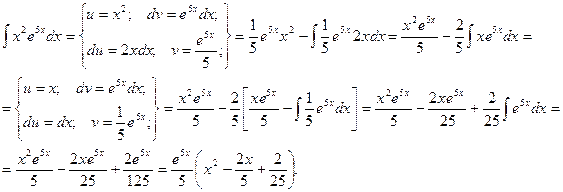
Пример.
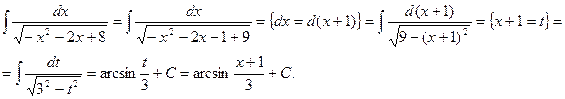
Пример.
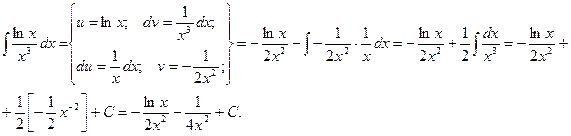
Пример.
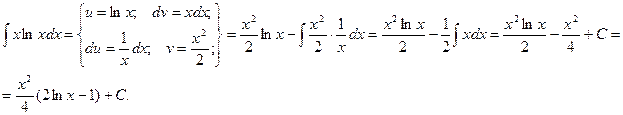
Пример.
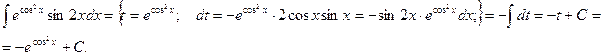
Пример.
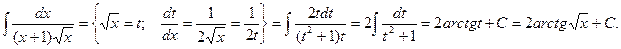
Пример.
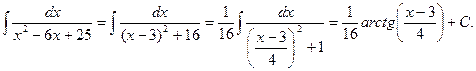
 2014-02-03
2014-02-03 1437
1437
