Первообразная. Неопределенный интеграл.
Определенный интеграл.
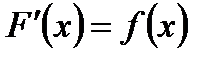 Функция F(x) называется первообразной для функции f(x) на промежутке I, если для любого х из промежутка I выполняется равенство:
Функция F(x) называется первообразной для функции f(x) на промежутке I, если для любого х из промежутка I выполняется равенство:
Для каждой функции существует множество первообразных Ф(х)=F(x)+c.
Неопределенный интеграл- это выражение, записанное в виде:
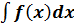 =F(x)+c
=F(x)+c
Сразу разбираемся в обозначениях и терминах:
 – значок интеграла.
– значок интеграла.
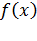 – подынтегральная функция
– подынтегральная функция
dx – значок дифференциала. При записи интеграла и в ходе решения важно не терять данный значок. Заметный недочет будет.
 – подынтегральное выражение или «начинка» интеграла.
– подынтегральное выражение или «начинка» интеграла.
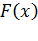 – первообразная функция.
– первообразная функция.
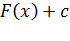 – множество первообразных функций (то есть, в любом неопределенном интеграле к ответу прибавляется с)
– множество первообразных функций (то есть, в любом неопределенном интеграле к ответу прибавляется с)
Решить интеграл – это значит найти определенную функцию, пользуясь некоторыми правилами, приемами и таблицей.
 Еще раз посмотрим на запись:
Еще раз посмотрим на запись:  .
.
Например:
 =3
=3 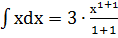 +с =
+с = 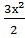 +с (Решаем по формуле 1 из таблицы. Можно сделать проверку, взяв производную полученного ответа!)
+с (Решаем по формуле 1 из таблицы. Можно сделать проверку, взяв производную полученного ответа!)
2. 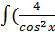 +
+  )dx= 4
)dx= 4 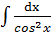 + 3
+ 3  = 4tg x+3
= 4tg x+3  2
2 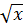 +c = 4tg x + 6
+c = 4tg x + 6 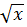 + c(
+ c( =2
=2 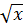 +c
+c
3.  dx=
dx= 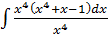 =
= 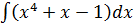 =
= 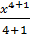 +
+  - x+c =
- x+c =  +
+ 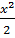 -x +c.
-x +c.
Определенным интегралом  в пределах от а до в от функции f(x), непрерывной на отрезке [ а, в ], называется приращение любой ее первообразной F(x) при изменении аргумента х от значения х=а до х=в:
в пределах от а до в от функции f(x), непрерывной на отрезке [ а, в ], называется приращение любой ее первообразной F(x) при изменении аргумента х от значения х=а до х=в:
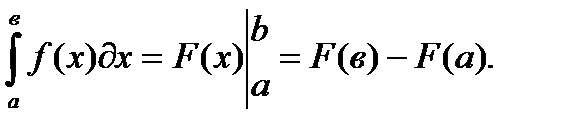
Данная формула так же называется формулой Ньютона-Лейбница, ее называют основной формулой интегрального исчисления.
ПРИМЕРЫ: Вычислить определенный интеграл:
1) 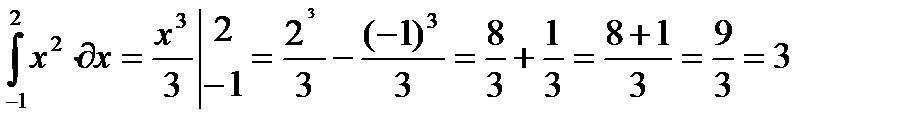 ;
;
 2022-01-07
2022-01-07 169
169







