Тема: Нахождение математического ожидания, дисперсии и среднего квадратичного отклонения дискретной случайной величины, заданной законом распределения

 

Практическое занятие № 8.

Цель: Научить вычислять математическое ожидание, дисперсию и среднее квадратичное отклонение дискретной случайной величины, заданной законом распределения.

 

Краткие теоретические сведения.

 

Случайное событие, связанное с некоторым опытом, является качественной характеристикой опыта. Количественной же характеристикой результата проведенного опыта является случайная величина.

Пример 1. Бросаются две правильные однородные монеты. Сколько из них выпадет гербом кверху?

При подбрасывании двух монет пространство элементарных событий имеет вид

                                        ,

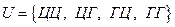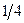Где Ц – «цифра», Г – «герб». Первый символ показывает, как выпала первая монета, а второй – вторая монета. Например, ЦГ означает, что первая монета выпала цифрой кверху, а вторая – гербом. Так как монеты правильные и однородные, то можно считать, что все элементарные события пространства  равновероятны, и тогда вероятность каждого из них равна . Обозначим через число монет, выпавших гербом кверху, и составим таблицу

                      

  

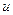
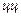
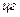
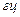
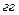
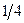
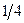
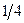
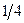
Так как элементарным событиям 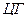и 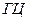соответствует одно и то же величины , равное 1, то можно полагать, что это значение величина принимает с вероятностью 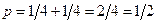. Таким образом, значения величины  - число монет, выпавшим гербом кверху, соответствующие им вероятности можно записать в виде таблицы.

                       

	0

 

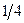
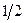
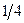
Итак, каждое значение величины есть число, определенное исходом опыта и зависит от случая.

Определение 1. Случайной называется величина, которая в результате опыта принимает с определенной вероятность то или иное значение, зависящее от исхода опыта.

Случайные величины обозначают прописными буквами латинского алфавита: 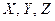 и т. д., а их значения – соответствующими строчными буквами:  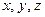и т. д.

Определение 2. Случайная величина называется дискретной, если множество ее значений конечно или счетно.

Вероятность того, что случайная величина  принимает значение , обозначают .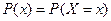

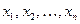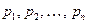Определение 3. Соответствие между возможными значениями  случайной величины и их вероятностями  называется законом распределения случайной величины .

 

Закон распределения случайной дискретной величины может быть представлен в виде таблицы.

                       Таблица 1.

 

                            

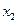
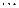
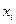
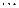
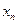
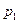
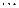
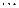
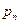
События 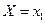, , , 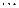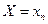образуют полную систему попарно несовместных событий, поэтому сумма их вероятностей равна единице.

                   .

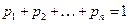Пример 2. Закон распределения вероятностей дискретной случайной величины  - число очков, выпадающих при бросании игральной кости, имеет вид, заданной таблицей.

                          

 

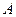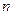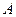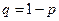Биноминальное распределение. Пусть случайная величина - число появления события  в  независимых испытаниях, в каждом из которых вероятность появления события  равна , а непоявления - . Очевидно, что  может принимать значения 0, 1, 2, 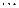, , 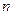вероятности которых определяются по формуле Бернулли:

.

Определение 4. Закон распределения случайной величины , имеющий вид

  

 

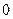
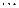
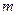
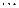
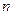
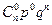
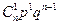
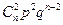
называется биноминальным распределением.

Пример 3. Составить закон распределения числа попаданий в цель при четырех выстрелах, если вероятность попадания при одном выстреле равна 0, 9.

Случайная величина  - число попаданий в цель при четырех выстрелах – может принимать значения 0, 1, 2, 3, 4, а соответствующие им вероятности находим по формуле Бернулли:

                              

                              

                              

                              

                              

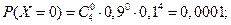
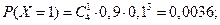
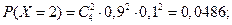
Итак, искомый закон распределения имеет вид

              

	0,0001	0,0036	0,0486	0,2916	0,6561

 

Математическое ожидание. Кроме закона распределения, который дает полное представление о случайной величине, часто используют числа, которые описывают случайную величину

 

 

суммарно. Такие числа называют числовыми характеристиками случайной величины. Среди числовых характеристик весьма важной является математическое ожидание, которое указывает, какое среднее значение случайной величины следует ожидать в результате испытаний или наблюдений.

Определение. Математическим ожиданием 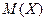дискретной случайной величины  называется сумма произведений всех ее возможных значений 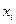 на их вероятность :

                (1)

Пример 4. Найти математическое ожидание случайной величины , зная закон ее распределения:

	-1
	0,2	0,1	0,25	0,15	0,3

           

 

По формуле (1) находим

.

Свойства математического ожидания.

1. Постоянный множитель можно выносить за знак математического ожидания:

                                   .

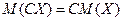2. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:

                                 

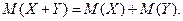
3. Математическое ожидание постоянной величины 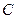 равно самой этой величине:

                                  .

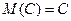4. Математическое ожидание линейной комбинации случайных величин равно линейной комбинации их математических ожиданий:

                                  

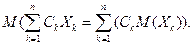
5. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:

                              

Дисперсия.

Рассмотрим пример.

Пример 5. Найти математическое ожидание случайных величин  и , зная закон их распределения.

    

 

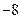
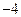
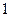
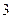
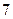
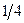
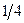
	-2

   

 

 

 

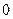
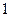
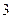
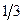
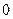
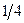
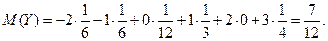
Мы получили, что законы распределения величин и разные, а их математические ожидания одинаковы.

Это произошло потому, что значения величины более сосредоточены около математического ожидания , чем значения величины , которые разбросаны (рассеяны) относительно ее математического ожидания 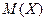. Основной числовой характеристикой степени рассеивания значений случайной величины относительно ее математического ожидания 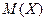является дисперсия, которая обозначается через .

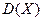Определение. Отклонением называется разность между случайной величиной и ее математическим ожиданием 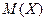, т.е.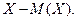

Затем, что отклонение 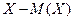 и его квадрат  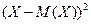также являются случайными величинами. Причем если случайная величина распределена по закону заданному таблицей 1, то квадрат ее отклонения имеет следующий закон распределения

 

 

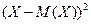
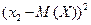
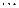
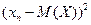
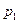
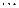
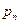
Определение. Дисперсией дискретной случайной величины называется математическое ожидание квадрата ее отклонения:

                                        .

Свойства дисперсии.

1. Дисперсия постоянной величины 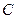 равна нулю:

                                                     .

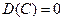2. Если -случайная величина, а 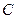 - постоянная, то

                                         

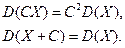
3. Если  и - независимые случайные величины, то

                                         

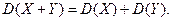
Для вычисления дисперсий более удобной является формула

                                      

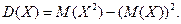
Пример 6. Дискретная случайная величина распределена по закону

	-1
	0,2	0,1	0,3	0,4

 

Найти .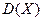

Сначала находим ,

а затем .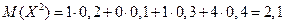

По формуле имеем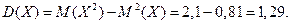

Величина 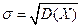 называется средним квадратичным отклонением.

                               

Задания для самостоятельной работы.

 

1. Дискретная случайная величина задана законом распределения

	0,1	0,4	0,5

 

	6	3
	0,2	0,3	0,5

 

	0,1	0,3	0,6

3)

1)     2) 

 

 

                                                                                                         

 

	5)		6)

	0,1	0,5	0,4

 

	0,2	0,3	0,5

 

	0,1	0,5	0,4

4)

 

 

			8) 8
	0,1	0,6	0,4

 

	-1
	0,2	0,6	0,8

 

	0,24	0,35	0,44

9)

7)

         

     

			11) 6
	0,14	0,25	0,28

 

	-2		12) 5
	1,2	1,8	2,0

 

	2,1	0,1	2,0

12)

10)   

12)

                                            

 

	-1	1	14) 2
	0,4	0,6	0,8

 

	1	2	15) 4
	0,1	0,4	0,5

 

	-2	0
	0,5	0,36	0,46

 13)

 

 

Найти математическое ожидание, дисперсию и среднее квадратичное отклонение дискретной случайной величины.

2. Найти математическое ожидание и дисперсию дискретной случайной величины 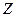, если известно, что

 1) , ,

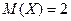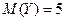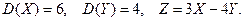
  2)

  3) .

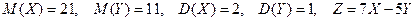  4)

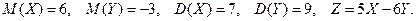
  5)

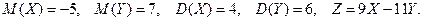
  6)

  7)

  8)

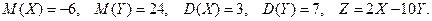
  9)

10)

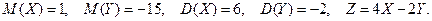
11)

12)

13)

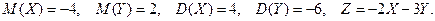
14)

15)

 

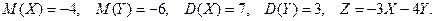
3. Вероятность отказа детали за время испытания на надежность равна 0,3. Найти числовые характеристики числа отказавших деталей, если испытанию будут подвергнуты 5 деталей.

4. В партии из 10 деталей содержится 3 нестандартных. Наудачу отобраны 2 детали. Найти числовые характеристики дискретной случайной величины Х – числа нестандартных деталей среди отобранных.

5. Вероятность отказа детали за время испытания на надежность равна 0,1. Найти числовые характеристики числа отказавших деталей, если испытанию будут подвергнуты 3 деталей.

6. В партии из 6 деталей имеется 4 стандартных. Наудачу отобраны 3 детали. Найти  числовые характеристики дискретной случайной величины Х – числа стандартных деталей среди отобранных.

7. В партии из 5 деталей имеется 3 окрашенных. Наудачу отобраны 2 детали. Найти числовые характеристики дискретной случайной величины Х – числа окрашенных деталей среди отобранных.

 

 

8. Вероятность отказа детали за время испытания на надежность равна 0,2. Найти числовые характеристики числа отказавших деталей, если испытанию будут подвергнуты 3 деталей.

9. Среди пяти ключей два подходят к двери. Ключи пробуют один за другим, пока не откроют дверь. Найти распределение вероятностей для числа опробованных ключей.

10. Стрелок стреляет по движущееся мишени до первого попадания в нее, причем успевает сделать не более четырех выстрелов. Найти числовые характеристики числа сделанных выстрелов, если вероятность попадания при каждом выстреле равна 0,6.

11. В шестиламповом радиоприемнике перегорела одна лампа. Лампы заменяют новыми одну за другой, пока приемник не заработает. Найти числовые характеристики числа замененных ламп.

12. Найти математическое ожидание и дисперсию суммы выпавших очков при бросании четырех игральных костей.

13. Два станка выпускают деталь с вероятностью брака 0,01 и 0,05 соответственно. В выборке одна деталь выпущена первым станком и две – вторым. Найти закон распределения для числа бракованных деталей.

14. Три стрелка с вероятностью попадания в цель при отдельном выстреле 0,7, 0,8 и 0,9 соответственно делают по одному выстрелу. Найти распределение вероятностей для общего числа попаданий.

15. Каждая из пяти лампочек имеет дефект с вероятностью 0,1 Дефектная лампочка при включении сразу перегорает, и ее заменяют новой. Построить закон распределения для числа опробованных ламп.

16. Среди 10 деталей три – нужного размера. Детали извлекают поочередно, по не подберут две детали нужного размера, при этом делают не более четырех проб. Найти распределение числа извлеченных деталей.

17. Монету подбрасывают до тех пор, пока герб не выпадет второй раз, при этом делают не более четырех проб. Найти распределение числа извлеченных деталей.