Министерство образования и науки Украины
Национальный технический университет
"Харьковский политехнический институт"
Факультет ФТ Кафедра Инженерная электрофизика
Специальность __________________________________
Контрольная работа №3
Тема: "Оптимизация стержневого молниеотвода защищающий группу сооружений"
Выполнил Коробко А.А.
группа _____
Харьков 2013
Условие задачи. Иметься группа, состоящая их трех сооружений, каждое из которых представляет собой прямую призму, показных на рис.1.1. Координаты боковых ребер сооружений и их высоты приведены в табл.1.1. В последних двух сторонах указаны min и max значения координат их всех объектов-сооружений. Требуется определить положение одиночного стрежневого МО, при котором его высота будет наименьшей из всех возможных МО минимальное высоты, защищающих систему сооружение. Требуемая надежность молниезащиты группы сооружение 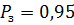 .
.
Решение. Так как высота оптимального МО при заданных условиях определяется двумя факторами X и Y – координатами его расположения, в качестве ядра ОЦКП второго порядка принимаем план ПФЕ 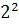 . Границы прямоугольной области исследования определим исходя из min и max значений координат объектов-стержней, приведенных в таблице 1.1. Проведем кодирование координат расположения МО с использованием (3.2). Учитывая, что для ОЦКП с ядром плана вида ПФЕ
. Границы прямоугольной области исследования определим исходя из min и max значений координат объектов-стержней, приведенных в таблице 1.1. Проведем кодирование координат расположения МО с использованием (3.2). Учитывая, что для ОЦКП с ядром плана вида ПФЕ 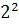
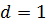 , границами области исследования будут являться нижний и верхний уровни изменения соответствующих факторов, Результаты кодирования приведены в таблице 1.2.
, границами области исследования будут являться нижний и верхний уровни изменения соответствующих факторов, Результаты кодирования приведены в таблице 1.2.
Рисунок 1.1 – План расположения сооружений:
1,2,3 –номера сооружений
Таблица 1.1 – Координаты ребер сооружений
| Номер сооружения | Номер Объекта-стержня | X координата расположения | Y координата расположения | Высота |
| 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 38 | 10 | 12 |
| 2 | 38 | 26 | ||
| 3 | 63 | 26 | ||
| 4 | 63 | 10 | ||
| 2 | 5 | 20 | 7 | 30 |
| 6 | 20 | 19 | ||
| 7 | 30 | 19 | ||
| 8 | 30 | 14 | ||
| 9 | 25 | 14 | ||
| 10 | 25 | 7 | ||
| 3 | 11 | 74 | 5 | 12 |
| 12 | 74 | 15 | ||
| 13 | 94 | 15 | ||
| 14 | 94 | 5 | ||
| min | 20 | 5 | ||
| max | 94 | 26 | ||
Таблица 1.2 – Кодирование факторов
| Наименование фактора | Обозначение фактора | Кодированное обозначение фактора | Интервал, hi | Уровни | ||
| -1 | 0 | 1 | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| X координата расположения | X | x1 | 37 | 20 | 57 | 94 |
| У координата расположения | Y | x2 | 10,5 | 5 | 15,5 | 26 |
В таблице 1.3 приведен ОЦКП для решения рассматриваемой задачи. Столбец 9 содержит 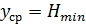 – высоты МО минимальной высоты, рассчитанные для соответственных уровней факторов, приведенных в столбцах 4 и 5. Вычисление
– высоты МО минимальной высоты, рассчитанные для соответственных уровней факторов, приведенных в столбцах 4 и 5. Вычисление 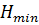 производиться в соответвии с шаговой процедурой, приведенной в описании задачи.
производиться в соответвии с шаговой процедурой, приведенной в описании задачи.
| Тип точек факторного пространства | Номер точки, u | x0 | x1 | x2 | x12-φ | x22-φ | x1*x2 | yср |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Точки ПФЭ | 1 | 1 | -1 | -1 | 1/3 | 1/3 | 1 | 75,5606 |
| 2 | 1 | 1 | -1 | 1/3 | 1/3 | -1 | 96,095 | |
| 3 | 1 | -1 | 1 | 1/3 | 1/3 | -1 | 77,437 | |
| 4 | 1 | 1 | 1 | 1/3 | 1/3 | 1 | 97,001 | |
| Звездные точки | 5 | 1 | -1 | 0 | 1/3 | - 2/3 | 0 | 75,6178 |
| 6 | 1 | 1 | 0 | 1/3 | - 2/3 | 0 | 95,409 | |
| 7 | 1 | 0 | -1 | - 2/3 | 1/3 | 0 | 66,301 | |
| 8 | 1 | 0 | 1 | - 2/3 | 1/3 | 0 | 67,995 | |
| Нулевая точка | 9 | 1 | 0 | 0 | - 2/3 | - 2/3 | 0 | 64,9699 |
| ∑ | 9 | 6 | 6 | 2 | 2 | 4 | 716,4 |
Таблица 1.4 – ОЦКП
Результаты дальнейших расчетов сведены в табл. 1.4. В последней строке таблицы приведены суммы всех элементов соответствующих столбцов, необходимы для определения 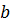 – коэффициентов.
– коэффициентов.
Таблица 1.4 – Результаты расчетов.
| x0*yср | x1*yср | x2*yср | (x12-φ)*yср | (x22-φ)*yср | x1x2*yср |
| 10 | 11 | 12 | 13 | 14 | 15 |
| 75,561 | -75,561 | -75,561 | 25,187 | 25,187 | 75,5606 |
| 96,095 | 96,095 | -96,095 | 32,032 | 32,032 | -96,095 |
| 77,437 | -77,437 | 77,437 | 25,812 | 25,812 | -77,437 |
| 97,001 | 97,001 | 97,001 | 32,334 | 32,334 | 97,001 |
| 75,618 | -75,618 | 0,000 | 25,206 | -50,412 | 0 |
| 95,409 | 95,409 | 0,000 | 31,803 | -63,606 | 0 |
| 66,301 | 0,000 | -66,301 | -44,201 | 22,100 | 0 |
| 67,995 | 0,000 | 67,995 | -45,330 | 22,665 | 0 |
| 65,0 | 0,0 | 0,0 | -43,3 | -43,3 | 0 |
| 716,39 | 59,89 | 4,48 | 39,53 | 2,80 | -0,97 |
Значения -коэффициентов, рассчитанные по формулам (1.18)...(1.21) [1], приведены в таблице 1.5.
Свободный член, для уравнения регрессии в стандартном виде (1.22) определяем по формуле (1.23).
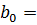 65,49
65,49
Таблица 1.5 – Значения коэффициентов
| b0* | b1 | b2 | b11 | b22 | b12 |
| 79,60 | 9,98 | 0,75 | 19,76 | 1,40 | -0,24 |
Далее произведем переход физическим переменным в соответствии с (3.4) [1]. Тогда, в конечном виде, уравнение для определения 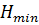 – высоты МО минимальной высоты в зависимости координат его расположения имеет вид:
– высоты МО минимальной высоты в зависимости координат его расположения имеет вид:
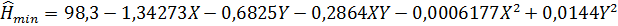
В табл. 1.6 приведен расчет погрешностей вычисления по уравнению регрессии
Последняя строка табл. 1.6 содержит значения максимальной абсолютной и относительной погрешности.
Таблица 1.6 – Расчет погрешностей
| X | Y | yср,расч. | δ | ?, % | yср,расч.2 | δ2 | ?2, % |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 20 | 5 | 75,68292222 | 0,122322222 | 0,161624603 | 75,629124 | 0,068524 | 0,090605 |
| 94 | 5 | 96,13132222 | 0,036322222 | 0,037783962 | 96,0369328 | 0,0580672 | 0,060463 |
| 20 | 26 | 77,66025556 | 0,223255556 | 0,287477235 | 77,6229648 | 0,1859648 | 0,239574 |
| 94 | 26 | 97,13825556 | 0,137255556 | 0,141299177 | 97,07077456 | 0,06977456 | 0,07188 |
| 20 | 15,5 | 75,27222222 | 0,345577778 | 0,459103993 | 75,2258694 | 0,3919306 | 0,521005 |
| 94 | 15,5 | 95,23542222 | 0,173577778 | 0,182261782 | 95,15367868 | 0,25532132 | 0,268325 |
| 57 | 5 | 66,14235556 | 0,158644444 | 0,239853031 | 66,1194284 | 0,1815716 | 0,274612 |
| 57 | 26 | 67,63448889 | 0,360511111 | 0,533028514 | 67,63326968 | 0,36173032 | 0,534841 |
| 57 | 15,5 | 65,48905556 | 0,519155556 | 0,792736361 | 65,47617404 | 0,50627404 | 0,773219 |
| max | 0,519155556 | 0,792736361 |
| 0,50627404 | 0,773219 | ||
| min | 0,036322222 | 0,037783962 |
| 0,0580672 | 0,060463 | ||
Учитывая, что определение 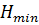 производиться численными методами и вычисление при параллельных опытах дают один и тот же результат, а значит, отсутствует возможность определить дисперсию воспроизводимости, адекватность полученной модели
производиться численными методами и вычисление при параллельных опытах дают один и тот же результат, а значит, отсутствует возможность определить дисперсию воспроизводимости, адекватность полученной модели 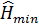 определим исходя из максимальной погрешности вычислений, приведены в табл. 1.6 Будем считать, что модель адекватна исходным данным с абсолютной погрешностью
определим исходя из максимальной погрешности вычислений, приведены в табл. 1.6 Будем считать, что модель адекватна исходным данным с абсолютной погрешностью 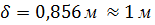
Определим координаты стационарной точки:
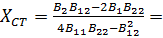 47,584
47,584
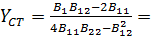 12,433
12,433
Стационарная точка находиться внутри исследуемой области. Исследуем стационарную точку на наличие экстремума.
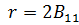
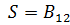
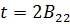
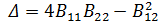
Так как 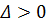 и
и 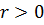 , то в стационарной точке имеет место минимум отклика. Если в этой точке установить МО, то н будет отвечать принятым условиям оптимальности. Из уравнения регрессии определим значение высоты в стационарной точке
, то в стационарной точке имеет место минимум отклика. Если в этой точке установить МО, то н будет отвечать принятым условиям оптимальности. Из уравнения регрессии определим значение высоты в стационарной точке 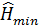 =64,097 м. Непосредственные расчеты с использованием пошаговой процедуры с
=64,097 м. Непосредственные расчеты с использованием пошаговой процедуры с 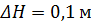 показывают, что МО. Размещенный в стационарной точке и защищающий группу сооружений, имеет
показывают, что МО. Размещенный в стационарной точке и защищающий группу сооружений, имеет 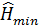 =81,3 м. Как видно, погрешность не превышает принятой в условиях адекватности модели.
=81,3 м. Как видно, погрешность не превышает принятой в условиях адекватности модели.
 2023-09-17
2023-09-17 1208
1208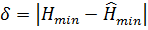 ;
;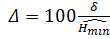 ;
;






