В горизонтальной плоскости характерными маневрами являются: разворот для изменения направления полёта (угла пути 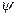 ); неустановившийся вираж – разворот самолёта на 360°; установившийся вираж с креном и скольжением; правильный вираж – установившийся вираж без скольжения.
); неустановившийся вираж – разворот самолёта на 360°; установившийся вираж с креном и скольжением; правильный вираж – установившийся вираж без скольжения.
Рассмотрим правильный вираж. Учитывая, что при правильном вираже: 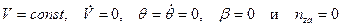 , из уравнений (2.17) получим уравнения движения центра масс самолёта в виде:
, из уравнений (2.17) получим уравнения движения центра масс самолёта в виде:
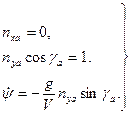 (7.11)
(7.11)
Так как 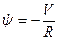 , то третье уравнение принимает вид
, то третье уравнение принимает вид
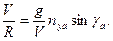 (7.12)
(7.12)
где R – радиус кривизны траектории движения центра масс самолёта.
Определим радиус правильного виража. Из (7.12) следует, что
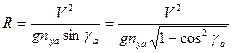 .
.
Подставив из второго уравнения системы (7.11) величину 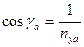 ,
,
будем иметь:
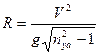 .
.
Отсюда видно, что с увеличением скорости радиус виража увеличивается, а с увеличением перегрузки 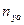 – уменьшается. Так как при правильном вираже:
– уменьшается. Так как при правильном вираже: 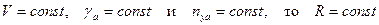 , т.е. самолёт описывает окружность с радиусом R. Следовательно, время
, т.е. самолёт описывает окружность с радиусом R. Следовательно, время 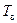 выполнения правильного виража:
выполнения правильного виража:
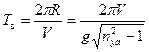 .
.
Из полученных выражений следует, что для определения всех параметров правильного виража 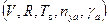 достаточно задать только две величины, например,
достаточно задать только две величины, например, 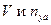 или
или 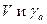 .
.
Рассмотрим границы области правильных виражей на плоскости 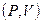 . Для определения границ области правильных виражей при заданной высоте Н построим кривые потребных тяг для различных значений
. Для определения границ области правильных виражей при заданной высоте Н построим кривые потребных тяг для различных значений 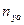 и кривую располагаемой тяги
и кривую располагаемой тяги 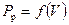 .
.
Из первого уравнения системы (7.11) следует, что правильный вираж представляет собой изоэнергетический маневр 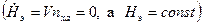 .
.
Ранее для изоэнергетического маневра были получены выражения (7.5) и (7.6).
Так как правильный вираж является изоэнергетическим маневром, то для построения кривых 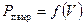 при различных значениях
при различных значениях 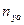 используем эти выражения в виде:
используем эти выражения в виде:
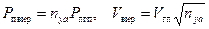 .
.
По результатам расчетов строим кривые (рисунок 7.4).
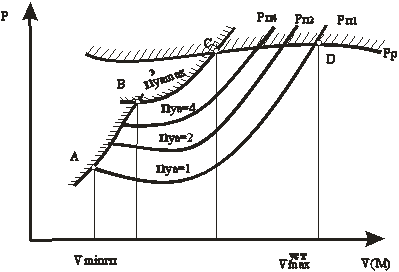
Рисунок 7.4 – Характеристики предельного виража
Границами области правильных виражей являются линии:
А-В – по безопасному значению 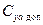 ;
;
В-С – по предельному значению 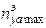 ;
;
С-D – по располагаемой тяге;
A-D – граница, соответствующая установившемуся прямолинейному горизонтальному полёту с 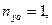 когда
когда 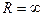 .
.
Область, заключенная между этими границами является областью правильных виражей. Каждой точке этой области будет соответствовать правильный вираж с однозначно определенными параметрами 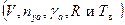 .
.
Построим график предельных виражей. Все точки, лежащие на границах правильных виражей, за исключением точек на границе (A-D) с перегрузкой 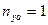 , соответствуют предельным виражам, выполняемым самолётом с предельными перегрузками
, соответствуют предельным виражам, выполняемым самолётом с предельными перегрузками 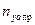 .
.
Рассчитать 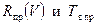 на данной высоте при
на данной высоте при 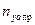 можно по формулам:
можно по формулам:
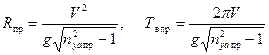 .
.
Определив по данным формулам 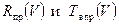 , можно построить график предельных виражей, например, для
, можно построить график предельных виражей, например, для 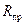 (рисунок 7.5).
(рисунок 7.5).
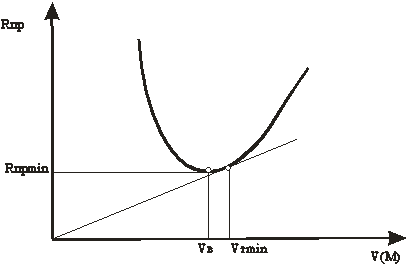
Рисунок 7.5 - График предельных виражей
Аналогичный график можно построить и для 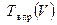 .
.
Из графика 7.5 видно, что на данной высоте полёта Н имеется минимум радиуса виража 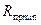 при скорости
при скорости 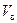 . Эта скорость называется наивыгоднейшей скоростью виража для данной высоты полёта.
. Эта скорость называется наивыгоднейшей скоростью виража для данной высоты полёта.
Скорость, при которой будет минимальное время выполнения виража 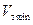 определится точкой касания прямой, проведённой из начала координат к кривой
определится точкой касания прямой, проведённой из начала координат к кривой 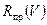 (рисунок 7.5). Имеем
(рисунок 7.5). Имеем 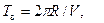 тогда
тогда 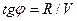 и
и 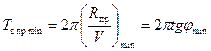 .
.
Из рисунка 7.5 видно, что 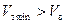 .
.
Рассмотрим неустановившийся вираж. При выполнении правильного виража для получения минимального радиуса или времени требуются небольшие скорости полёта при вводе в вираж. Если до начала выполнения правильного виража самолёт летел с большой скоростью, то для реализации правильного виража с 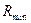 или
или 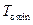 надо предварительно уменьшить скорость прямолинейного полёта до
надо предварительно уменьшить скорость прямолинейного полёта до 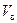 или
или 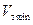 . Для более эффективного маневра целесообразно в процессе торможения осуществлять разворот. При этом движение самолёта будет неустановившемся.
. Для более эффективного маневра целесообразно в процессе торможения осуществлять разворот. При этом движение самолёта будет неустановившемся.
Для расчета параметров неустановившегося виража без скольжения используются уравнения:
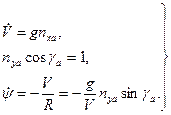 (7.13)
(7.13)
Из первого уравнения следует, что для уменьшения скорости 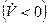 тангенциальная перегрузка
тангенциальная перегрузка 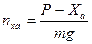 должна быть отрицательной, т.е.
должна быть отрицательной, т.е. 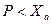 . Из второго и третьего уравнений получим выражение для мгновенного радиуса разворота
. Из второго и третьего уравнений получим выражение для мгновенного радиуса разворота
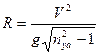 .
.
Если неустановившийся вираж выполняется с наименьшим радиусом разворота и торможением, то он называется форсированным. Для ввода самолёта в форсированный вираж надо уменьшать тягу двигателей и накренить самолёт на угол 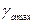 , создавая предельную нагрузку
, создавая предельную нагрузку 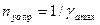 .
.
На первом этапе маневр выполняется с постоянной предельной перегрузкой: 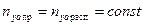 . При этом угол атаки a и коэффициент подъемной силы
. При этом угол атаки a и коэффициент подъемной силы 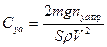 из-за уменьшения скорости должны увеличиваться до допустимого (безопасного) значения: a = aдопи
из-за уменьшения скорости должны увеличиваться до допустимого (безопасного) значения: a = aдопи 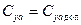 .
.
Поскольку при дальнейшем уменьшении скорости увеличение угла атаки недопустимо, то на втором этапе маневр продолжается при 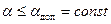 . При этом угол крена
. При этом угол крена 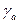 и перегрузка
и перегрузка 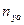 должны уменьшаться. В конце маневра угол крена должен быть равным нулю, а перегрузка
должны уменьшаться. В конце маневра угол крена должен быть равным нулю, а перегрузка 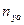 равна единице. Расчёт параметров неустановившегося виража проводится численным интегрированием уравнений (7.13). За независимую переменную целесообразно принять угол поворота траектории
равна единице. Расчёт параметров неустановившегося виража проводится численным интегрированием уравнений (7.13). За независимую переменную целесообразно принять угол поворота траектории 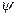 .
.
Траектория неустановившегося виража показана на рис. 7.6.
рис 7.6 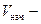 начальная скорость,
начальная скорость,

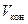 – конечная скорость,
– конечная скорость,
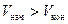 .
.
 2021-08-27
2021-08-27 199
199






