В поля, создаваемого отрезком бесконечно длинного провода L провода в точке A, удаленной от отрезка на расстояние r0. Сила тока, текущего по проводу, I, углы 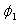 и
и 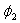 заданы.
заданы.
Сделаем рисунок:
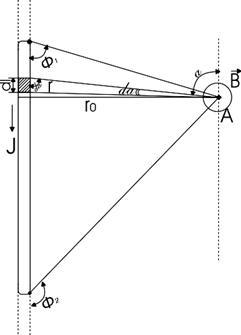
l - длина отрезка провода с током;
dl - длина элемента проводника;
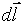 - вектор равный по модулю и совпадающий по направлению с током;
- вектор равный по модулю и совпадающий по направлению с током;
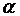 - угол между векторами
- угол между векторами 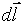 и
и  .
.
r0- длина перпендикуляра, опущенного из точки А на отрезок проводника с током;
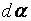 - приращение угла при перемещении по проводнику с током на расстояние dl.
- приращение угла при перемещении по проводнику с током на расстояние dl.
Решение:
Эту задачу решим, применяя закон Био-Савара-Лапласа в дифференциальной форме, метод дифференцирования и интегрирования и принцип cуперпозиции. Разобьем отрезок провода на элементарные отрезки длиной dl, для каждого из элементарных отрезков dl в искомой точке А найдем значение dB (согласно закону Био-Савара-Лапласа), а затем по принципу суперпозиции рассчитаем ВА.
Согласно закону Био-Савара-Лапласа в интегральной форме:
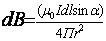 . . | (1) |
Рассмотрим ДСЕ. 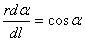 . Из ДОА:
. Из ДОА: 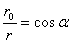 .
.
Тогда: 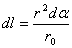 . Подставив выражение dl в формулу (1), получаем:
. Подставив выражение dl в формулу (1), получаем:
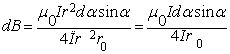 . . | (2) |
При перемещении по отрезку угол 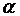 меняется от
меняется от 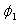 до
до 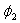 , тогда согласно принципу суперпозиции:
, тогда согласно принципу суперпозиции:
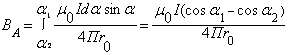 .
.
Отсюда: 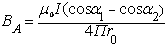 .
.
Вектор ВА направлен перпендикулярно плоскости листа острием на нас. 
Проверка размерности: 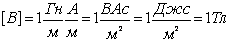 .
.
Ответ: 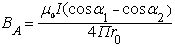 (Тл).
(Тл).
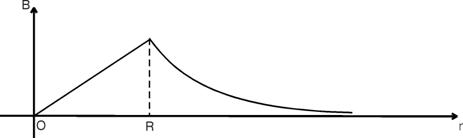
Пример №2. По сплошному бесконечному цилиндрическому проводнику радиуса R течет ток плотности j. Рассчитать магнитное поле внутри и вне проводника. Построить график зависимости B = f (r).
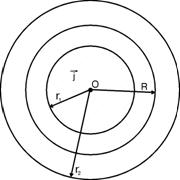
| Дано: | Решение: |
| R r1<R r2>R j | Проводник не тонкий, тогда закон Био-Савара-Лапласа неприменим. Однако поле обладает симметрией, поэтому применим теорему о циркуляции 1. В качестве замкнутого контура возьмем окружность радиуса r1, r1<R. Тогда модуль вектора магнитной индукции В1 в точке А1, расположенной на расстоянии r1 от оси проводника равен: |
| B1-? B2-? |
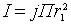 и
и 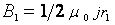 .
.
2. Если точку А2 возьмем вне проводника, а в качестве замкнутого контура возьмем окружность радиуса r2>R, тогда 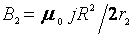
График зависимости В = f (r)имеет вид:
Ответ: 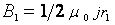 ;
; 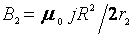 .
.
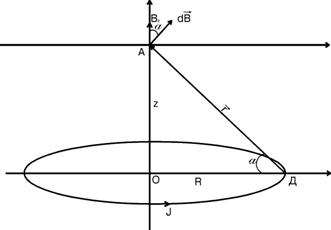
Пример №3. По проводнику в виде тонкого кольца радиусом R течет ток силой I. Найти индукцию магнитного поля на оси кругового тока: 1) на расстоянии z от плоскости кольца; 2) в центре кольца.
| Дано: | Решение: |
| I R z | 1) Применим метод ДИ. Разобьем кольцо на отрезки длиной dl. Согласно закону Био-Савара-Лапласа определим индукцию магнитного поля dB, созданного элементом кольца в точке А. Вектор |
| BА-? Bо-? |
От всех элементов тока кольца будет образовываться конус векторов 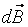 , а результирующий вектор
, а результирующий вектор 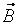 в точке А будет направлен вдоль оси z. Тогда:
в точке А будет направлен вдоль оси z. Тогда: 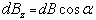 ,
, 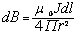 ;
;
Угол между 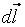 и радиусом-вектором
и радиусом-вектором 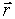 равен
равен  , т.е.
, т.е. 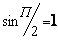 .
.
Для dBz получаем: 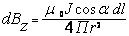 ;
; 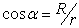 и
и
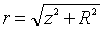 ;
; 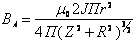 .
.
Проверка: 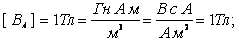
2) В центре кольца z=0, тогда 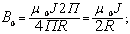
Ответ: 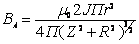 ;
; 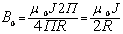 .
.
Пример №4. Тонкая лента шириной l свернута в трубку радиусом R. По ленте течет равномерно распределенный по ее ширине ток силой I. Определить индукцию магнитного поля В на оси трубки в двух точках: 1) В средней точке (1);2) В точке, совпадающей с концом трубки (2).
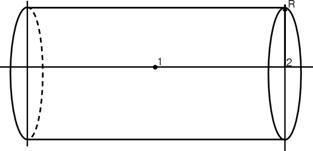
| Дано: | Решение: |
| I R l |
Проводник нельзя считать тонким, а теорема о циркуляции неприменима из-за отсутствия симметрии поля. Для расчета применим метод ДИ. Разобьем трубку на столь узкие кольца, чтобы каждое из них можно было считать тонким круговым проводником. Пусть ширина кольца - dx, а расстояние от кольца до точки (1) - x. Сделаем рисунок: |
| B 1-? B 2-? |

Тогда элементарный ток, текущий по этому узкому кольцу равен:
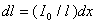 , где
, где 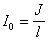 - ток, приходящийся на единицу длины трубки. Он создает в точке (1) магнитное поле с индукцией dB1.
- ток, приходящийся на единицу длины трубки. Он создает в точке (1) магнитное поле с индукцией dB1. 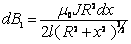
За переменную интегрирования удобно выбрать угол 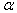 , под которым виден радиус каждого кольца из точки (1). Тогда из рисунка следует:
, под которым виден радиус каждого кольца из точки (1). Тогда из рисунка следует: 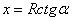 ;
; 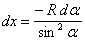 ;
; 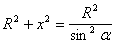 .
.
Тогда: 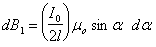 .
.
При перемещении по трубке от точки (0) до точки (1) угол 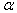 меняется в следующих пределах: от
меняется в следующих пределах: от 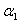 до
до 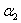 , причем
, причем 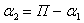 .
.
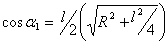 ;
; 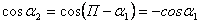 .
.
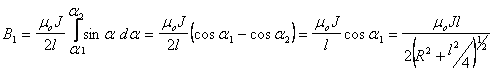
Во втором случае: 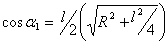 ;
; 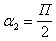 ; и тогда
; и тогда
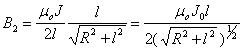
Проверка: 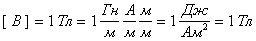 ;
;
Ответ: 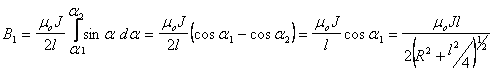 ,
, 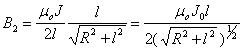 .
.
Пример №5. Два бесконечно длинных, параллельных провода, по которым текут в одном направлении токи силой 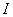 = 60 А, расположены на расстоянии
= 60 А, расположены на расстоянии 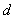 = 10 см друг от друга. Определить магнитную индукцию
= 10 см друг от друга. Определить магнитную индукцию 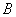 в точке, отстоящей от одного проводника на расстоянии
в точке, отстоящей от одного проводника на расстоянии 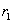 = 5 см и от другого на расстоянии
= 5 см и от другого на расстоянии 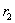 = 12 см.
= 12 см.
| Дано: | Решение: | |
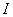 = 60 A = 60 A 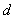 = 10 см = 10 см 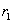 = 5 см = 5 см 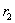 = 12 см = 12 см | Для нахождения магнитной индукции в указанной точке А, определим направление векторов индукции | |
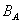 =? =? | ||
 . . | (1) | |
Значения индукции 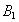 и
и 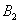 выражаются соответственно через силу тока
выражаются соответственно через силу тока 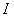 и расстояния
и расстояния 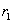 и
и 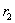 от провода до точки, индукцию в которой вычислим как:
от провода до точки, индукцию в которой вычислим как: 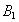 =
= 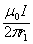 ;
; 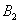 =
= 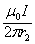 .
.
Подставив эти выражения в (1) и вынеся 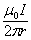 из под знака корня, получим:
из под знака корня, получим:
 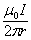 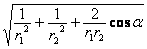 . . | (2) |
Вычислим 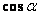 ; (
; ( =ÐDAC) по теореме косинусов:
=ÐDAC) по теореме косинусов: 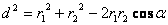 ,=>
,=> 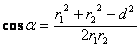 ;
; 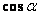 =0,576
=0,576
Расчёт: 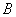 = 286 мкТл;
= 286 мкТл;
Ответ: 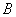 = 286 мкТл.
= 286 мкТл.
Пример №6. По двум длинным прямолинейным проводам, находящимся на расстоянии 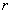 = 5 см друг от друга в воздухе, текут токи силой
= 5 см друг от друга в воздухе, текут токи силой 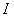 = 10 А каждый. Определить магнитную индукцию
= 10 А каждый. Определить магнитную индукцию 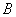 поля, создаваемого токами в точке, лежащей посередине между проводами для случаев:
поля, создаваемого токами в точке, лежащей посередине между проводами для случаев:
1. провода параллельны, токи текут в одном направлении (см. рис. 1);
2. провода параллельны, токи текут в противоположных направлениях (см. рис. 2);
3. провода перпендикулярны (см. рис. 3).
| Дано: | Решение: |
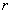 = 5 см = 5 см 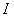 = 10A = 10A | Результирующая индукция равна векторной сумме:
Если
|
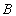 =? =? |
быть замена алгебраической:
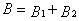 , , | (1) |
при этом слагаемые 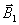 и
и  должны быть взяты с соответствующими знаками.
должны быть взяты с соответствующими знаками.
В данной задаче во всех трёх случаях абсолютные значения В1 и В2 одинаковы, так как точки выбраны на равных расстояниях от проводов, по которым текут равные токи.
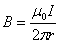 . . | (2) |
Рассчитаем: 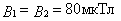
1 случай
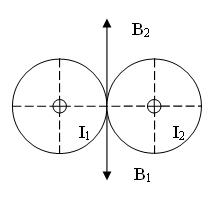
Рис. 1
Векторы 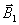 и
и  направлены по одной прямой, следовательно результирующая индукция В определяется по формуле (1) Приняв направление вверх положительным, вниз - отрицательным:
направлены по одной прямой, следовательно результирующая индукция В определяется по формуле (1) Приняв направление вверх положительным, вниз - отрицательным: 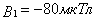 ,
, 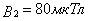 , подставим в (1)
, подставим в (1) 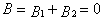
2 случай
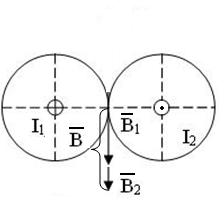
Рис. 2
Векторы 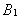 и
и 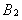 направлены по одной прямой в одну сторону.
направлены по одной прямой в одну сторону.
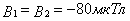
Подставим в (1): 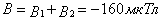
3 случай
Рис. 3
Векторы индукции магнитных полей, создаваемых токами в точке, лежащей посередине между проводами взаимно перпендикулярны.
Результирующая индукция по абсолютному значению и направлению является диагональю квадрата, построенного на векторах 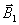 и
и  .
.
По теореме Пифагора:
 . . | (3) |
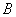 = 113 мкТл.
= 113 мкТл.
Ответ: 1) 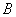 = 0; 2)
= 0; 2) 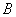 = -160 мкТл; 3)
= -160 мкТл; 3) 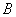 = 113 мкТл.
= 113 мкТл.
Пример №7. По проводнику согнутому в виде квадратной рамки со стороной a = 10 см, течёт ток силой 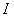 = 5 A. Определить магнитную индукцию
= 5 A. Определить магнитную индукцию 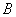 поля в точке, равноудалённой от вершины квадрата на расстояние, равное длине его стороны.
поля в точке, равноудалённой от вершины квадрата на расстояние, равное длине его стороны.
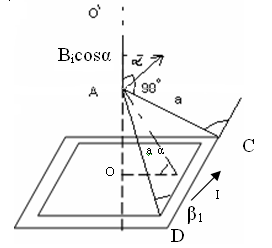
| Дано: | Решение: |
 = 10 см = 10 см 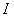 = 5 A = 5 A | Искомая магнитная индукция |
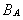 =? =? |
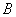 =
= 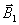 +
+  +
+ 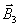 +
+ 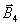 .
.
Из соображений симметрии абсолютные значения всех четырёх индукции одинаковы (поэтому на рисунке изображён только один вектор 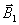 . В соответствии с правилами буравчика вектор
. В соответствии с правилами буравчика вектор 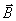 перпендикулярен плоскости ΔADC). Результирующий вектор
перпендикулярен плоскости ΔADC). Результирующий вектор 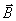 будет направлен вдоль оси ОО” и равен сумме проекций всех векторов на направление этой оси, т.е.
будет направлен вдоль оси ОО” и равен сумме проекций всех векторов на направление этой оси, т.е. 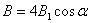 .
.
Из рисунка следует, что 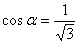 ,
,
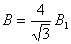 . . | (1) |
Магнитная индукция поля, создаваемая отрезком проводника:
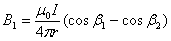 , , | (2) |
где I – сила тока в проводнике; 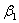 и
и 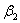 – углы, образованные направлением тока и радиус-векторами, проведёнными от концов проводника к т. А (
– углы, образованные направлением тока и радиус-векторами, проведёнными от концов проводника к т. А (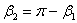 ), следовательно
), следовательно 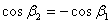 , тогда:
, тогда:
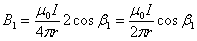 , , | (3) |
подставим (3) в (1):
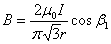 . . | (4) |
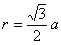 ,
, 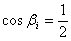 (т.к.
(т.к. 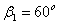 )
)
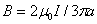 . . | (5) |
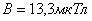 .
.
Ответ: 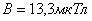 .
.
 2021-09-14
2021-09-14 857
857






