В Примере 1 скалярное произведение получилось положительным, а в Примере 2 – отрицательным. Выясним, от чего зависит знак скалярного произведения. Смотрим на нашу формулу: 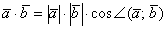 . Длины ненулевых векторов всегда положительны:
. Длины ненулевых векторов всегда положительны: 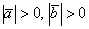 , поэтому знак может зависеть только от значения косинуса.
, поэтому знак может зависеть только от значения косинуса.
Примечание: Для более качественного понимания нижеприведенной информации лучше изучить график косинуса в методичке Графики и свойства функции. Посмотрите, как ведёт себя косинус на отрезке 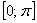 .
.
Как уже отмечалось, угол между векторами может изменяться в пределах 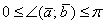 , и при этом возможны следующие случаи:
, и при этом возможны следующие случаи:
1) Если угол между векторами острый: 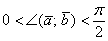 (от 0 до 90 градусов), то
(от 0 до 90 градусов), то 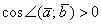 , и скалярное произведение будет положительным:
, и скалярное произведение будет положительным: 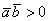 . Особый случай: если векторы сонаправлены, то угол между ними считается нулевым
. Особый случай: если векторы сонаправлены, то угол между ними считается нулевым 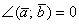 , и скалярное произведение также будет положительным. Поскольку
, и скалярное произведение также будет положительным. Поскольку 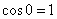 , то формула упрощается:
, то формула упрощается: 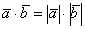 .
.
2) Если угол между векторами тупой: 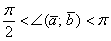 (от 90 до 180 градусов), то
(от 90 до 180 градусов), то 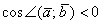 , и, соответственно, скалярное произведение отрицательно:
, и, соответственно, скалярное произведение отрицательно: 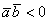 . Особый случай: если векторы направлены противоположно, то угол между ними считается развёрнутым:
. Особый случай: если векторы направлены противоположно, то угол между ними считается развёрнутым: 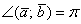 (180 градусов). Скалярное произведение тоже отрицательно, так как
(180 градусов). Скалярное произведение тоже отрицательно, так как 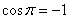
Справедливы и обратные утверждения:
1) Если 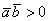 , то угол между данными векторами острый. Как вариант, векторы сонаправлены.
, то угол между данными векторами острый. Как вариант, векторы сонаправлены.
2) Если 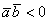 , то угол между данными векторами тупой. Как вариант, векторы направлены противоположно.
, то угол между данными векторами тупой. Как вариант, векторы направлены противоположно.
Но особый интерес представляет третий случай:
3) Если угол между векторами прямой: 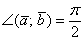 (90 градусов), то
(90 градусов), то 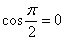 и скалярное произведение равно нулю:
и скалярное произведение равно нулю: 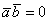 . Обратное тоже верно: если
. Обратное тоже верно: если 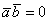 , то
, то 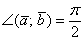 . Компактно утверждение формулируется так: Скалярное произведение двух векторов равно нулю тогда и только тогда, когда данные векторы ортогональны. Короткая математическая запись:
. Компактно утверждение формулируется так: Скалярное произведение двух векторов равно нулю тогда и только тогда, когда данные векторы ортогональны. Короткая математическая запись: 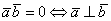
! Примечание: Рекомендую запомнить математический значок 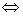 , в математике его обычно читают: «тогда и только тогда», «в том и только в том случае». Как видите, стрелки направлены в обе стороны – «из этого следует это, и обратно – из того, следует это». В чём, кстати, отличие от одностороннего значка следования
, в математике его обычно читают: «тогда и только тогда», «в том и только в том случае». Как видите, стрелки направлены в обе стороны – «из этого следует это, и обратно – из того, следует это». В чём, кстати, отличие от одностороннего значка следования 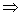 ? Значок
? Значок 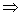 утверждает, только то, что «из этого следует это», и не факт, что обратное справедливо. Например:
утверждает, только то, что «из этого следует это», и не факт, что обратное справедливо. Например: 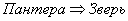 , но не каждый зверь является пантерой, поэтому в данном случае нельзя использовать значок
, но не каждый зверь является пантерой, поэтому в данном случае нельзя использовать значок 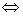 . В то же время, вместо значка
. В то же время, вместо значка 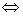 можно использовать односторонний значок. Например, решая задачу, мы выяснили, что
можно использовать односторонний значок. Например, решая задачу, мы выяснили, что 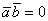 и сделали вывод, что векторы ортогональны:
и сделали вывод, что векторы ортогональны: 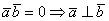 – такая запись будет корректной, и даже более уместной, чем
– такая запись будет корректной, и даже более уместной, чем 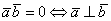 .
.
Третий случай имеет большую практическую значимость, поскольку позволяет проверить, ортогональны векторы или нет. Данную задачу мы решим во втором разделе урока.
Скалярный квадрат вектора
Свойства скалярного произведения
Вернёмся к ситуации, когда два вектора сонаправлены. В этом случае угол между ними равен нулю, 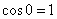 , и формула скалярного произведения принимает вид:
, и формула скалярного произведения принимает вид: 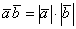 .
.
А что будет, если вектор 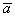 умножить на самого себя? Понятно, что вектор сонаправлен сам с собой, поэтому пользуемся вышеуказанной упрощенной формулой:
умножить на самого себя? Понятно, что вектор сонаправлен сам с собой, поэтому пользуемся вышеуказанной упрощенной формулой:
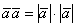
Или: 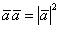
Число 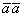 называется скалярным квадратом вектора
называется скалярным квадратом вектора 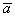 , и обозначатся как
, и обозначатся как 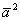 .
.
Таким образом, скалярный квадрат вектора 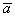 равен квадрату длины данного вектора:
равен квадрату длины данного вектора:
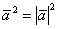
Из данного равенства можно получить формулу для вычисления длины вектора:
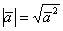
Пока она кажется малопонятной, но задачи урока всё расставят на свои места. Для решения задач нам также потребуются свойства скалярного произведения.
Для произвольных векторов 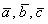 и любого числа
и любого числа 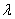 справедливы следующие свойства:
справедливы следующие свойства:
1) 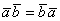 – переместительный или коммутативный закон скалярного произведения.
– переместительный или коммутативный закон скалярного произведения.
2) 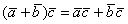 – распределительный или дистрибутивный закон скалярного произведения. Попросту, можно раскрывать скобки.
– распределительный или дистрибутивный закон скалярного произведения. Попросту, можно раскрывать скобки.
3) 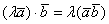 – сочетательный или ассоциативный закон скалярного произведения. Константу можно вынести из скалярного произведения.
– сочетательный или ассоциативный закон скалярного произведения. Константу можно вынести из скалярного произведения.
Зачастую, всевозможные свойства (которые ещё и доказывать надо!) воспринимаются студентами как ненужный хлам, который лишь необходимо вызубрить и сразу после экзамена благополучно забыть. Казалось бы, чего тут важного, все и так с первого класса знают, что от перестановки множителей произведение не меняется: 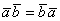 . Должен предостеречь, в высшей математике с подобным подходом легко наломать дров. Так, например, переместительное свойство не является справедливым для алгебраических матриц. Неверно оно и для векторного произведения векторов. Поэтому, в любые свойства, которые вам встретятся в курсе высшей математики, как минимум, лучше вникать, чтобы понять, что можно делать, а чего нельзя.
. Должен предостеречь, в высшей математике с подобным подходом легко наломать дров. Так, например, переместительное свойство не является справедливым для алгебраических матриц. Неверно оно и для векторного произведения векторов. Поэтому, в любые свойства, которые вам встретятся в курсе высшей математики, как минимум, лучше вникать, чтобы понять, что можно делать, а чего нельзя.
Пример 3
Найти скалярное произведение векторов 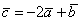 и
и 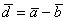 , если известно, что
, если известно, что 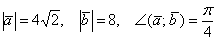 .
.
Решение: Сначала проясним ситуацию с вектором 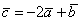 . Что это вообще такое? Сумма векторов
. Что это вообще такое? Сумма векторов 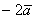 и
и 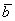 представляет собой вполне определенный вектор, который и обозначен через
представляет собой вполне определенный вектор, который и обозначен через 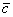 . Геометрическую интерпретацию действий с векторами можно найти в статье Векторы для чайников. Та же петрушка с вектором
. Геометрическую интерпретацию действий с векторами можно найти в статье Векторы для чайников. Та же петрушка с вектором 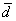 – это сумма векторов
– это сумма векторов 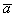 и
и 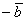 .
.
Итак, по условию требуется найти скалярное произведение 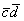 . По идее, нужно применить рабочую формулу
. По идее, нужно применить рабочую формулу 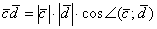 , но беда в том, что нам неизвестны длины векторов
, но беда в том, что нам неизвестны длины векторов 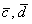 и угол между ними. Зато в условии даны аналогичные параметры для векторов
и угол между ними. Зато в условии даны аналогичные параметры для векторов 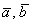 , поэтому мы пойдём другим путём:
, поэтому мы пойдём другим путём:
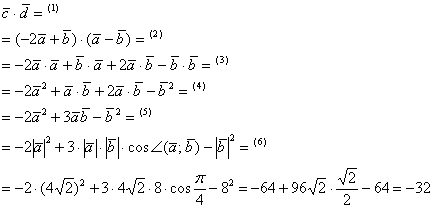
(1) Поставляем выражения векторов 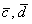 .
.
(2) Раскрываем скобки по правилу умножения многочленов, пошлую скороговорку можно найти в статье Комплексные числа или Интегрирование дробно-рациональной функции. Повторяться уж не буду =) Кстати, раскрыть скобки нам позволяет дистрибутивное свойство скалярного произведения. Имеем право.
(3) В первом и последнем слагаемом компактно записываем скалярные квадраты векторов: 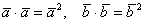 . Во втором слагаемом используем перестановочность скалярного произведения:
. Во втором слагаемом используем перестановочность скалярного произведения: 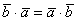 .
.
(4) Приводим подобные слагаемые: 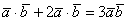 .
.
(5) В первом слагаемом используем формулу скалярного квадрата 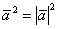 , о которой не так давно упоминалось. В последнем слагаемом, соответственно, работает та же штука:
, о которой не так давно упоминалось. В последнем слагаемом, соответственно, работает та же штука: 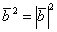 . Второе слагаемое раскладываем по стандартной формуле
. Второе слагаемое раскладываем по стандартной формуле 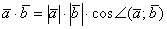 .
.
(6) Подставляем данные условия 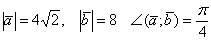 , и ВНИМАТЕЛЬНО проводим окончательные вычисления.
, и ВНИМАТЕЛЬНО проводим окончательные вычисления.
Ответ: 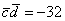
Отрицательное значение скалярного произведения констатирует тот факт, что угол между векторами 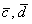 является тупым.
является тупым.
Задача типовая, вот пример для самостоятельного решения:
Пример 4
Найти скалярное произведение векторов 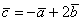 и
и 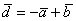 , если известно, что
, если известно, что 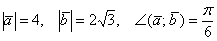 .
.
Краткое решение и ответ в конце урока.
Теперь ещё одно распространённое задание, как раз на новую формулу длины вектора 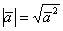 . Обозначения тут будут немного совпадать, поэтому для ясности я перепишу её с другой буквой:
. Обозначения тут будут немного совпадать, поэтому для ясности я перепишу её с другой буквой: 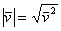
Пример 5
Найти длину вектора 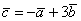 , если
, если 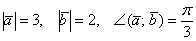 .
.
Решение будет следующим:
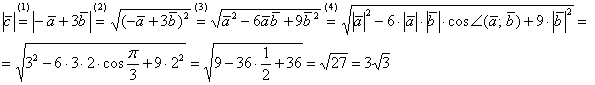
(1) Поставляем выражение вектора 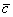 .
.
(2) Используем формулу длины: 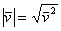 , при этом в качестве вектора «вэ» у нас выступает целое выражение
, при этом в качестве вектора «вэ» у нас выступает целое выражение 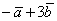 .
.
(3) Используем школьную формулу квадрата суммы 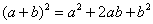 . Обратите внимание, как она здесь любопытно работает:
. Обратите внимание, как она здесь любопытно работает: 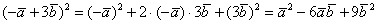 – фактически это квадрат разности, и, по сути, так оно и есть. Желающие могут переставить векторы местами:
– фактически это квадрат разности, и, по сути, так оно и есть. Желающие могут переставить векторы местами: 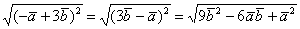 – получилось то же самое с точностью до перестановки слагаемых.
– получилось то же самое с точностью до перестановки слагаемых.
(4) Дальнейшее уже знакомо из двух предыдущих задач.
Ответ: 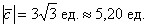
Коль скоро речь идёт о длине, не забываем указать размерность – «единицы».
Пример 6
Найти длину вектора 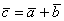 , если
, если 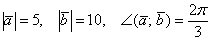 .
.
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
 2015-08-13
2015-08-13 3978
3978
