В 1820 г. Био и Савар исследовали магнитные поля, создаваемые токами, текущими по тонким проводам различной формы. Путем анализа этих экспериментальных данных Лаплас установил закон, получивший название закона Био-Савара-Лапласа:
1) Магнитное поле любого тока может быть найдено как векторная сумма полей, создаваемых отдельными элементарными участками тока. Каждый элемент тока характеризуется величиной 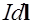 , где
, где 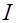 - сила тока, текущего в этом элементе,
- сила тока, текущего в этом элементе, 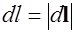 - длина элемента тока, а вектор
- длина элемента тока, а вектор 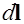 указывает направление тока.
указывает направление тока.
2) Для магнитной индукции поля, создаваемого элементом тока 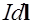 Лаплас получил выражение
Лаплас получил выражение
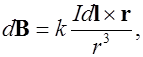 (6.4)
(6.4)
где 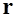 - радиус-вектор, проведенный из точки расположения элемента тока в точку наблюдения, где определяется индукция
- радиус-вектор, проведенный из точки расположения элемента тока в точку наблюдения, где определяется индукция 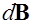 ,
, 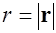 (см. рис. 6.3),
(см. рис. 6.3), 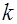 - коэффициент пропорциональности, зависящий от выбора единиц измерения и магнитных свойств среды, где протекает ток; в системе СИ для вакуума
- коэффициент пропорциональности, зависящий от выбора единиц измерения и магнитных свойств среды, где протекает ток; в системе СИ для вакуума
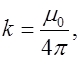
где 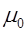 - магнитная проницаемость вакуума, измеряемая в
- магнитная проницаемость вакуума, измеряемая в 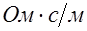 .
.
Модуль выражения (6.4) равен
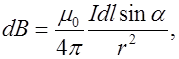 (6.5)
(6.5)
где 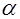 - угол между векторами
- угол между векторами 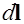 и
и 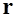 .
.
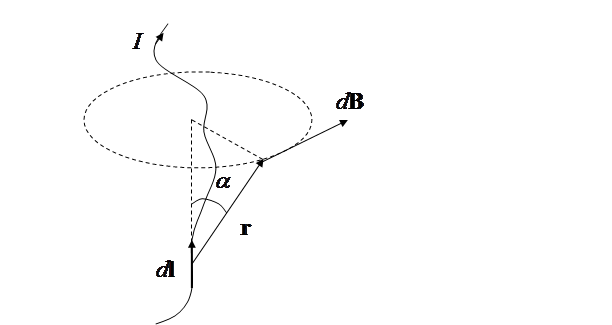
Рис. 6.3. К формулировке закона Био-Савара-Лапласа
Применим формулу (6.5) для вычисления магнитного поля, создаваемого током, текущим по тонкому прямолинейному проводу теоретически бесконечной длины (см. рис. 6.4).
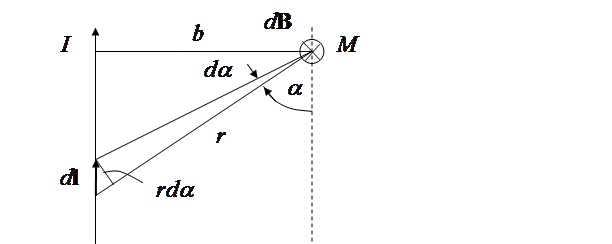
Рис. 6.4.
Векторы 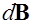 от всех элементов тока
от всех элементов тока 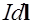 прямолинейного провода в точке наблюдения
прямолинейного провода в точке наблюдения 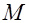 направлены одинаково – за плоскость чертежа. Точка наблюдения
направлены одинаково – за плоскость чертежа. Точка наблюдения 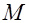 находится на расстоянии
находится на расстоянии 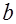 от провода. Согласно рис. 6.4,
от провода. Согласно рис. 6.4,
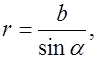
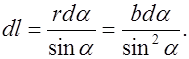
Эти выражения подставим в (6.5):
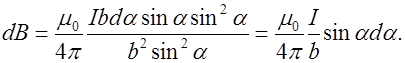
При движении вдоль провода угол 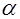 изменяется в пределах от
изменяется в пределах от 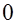 до
до 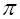 . Поэтому
. Поэтому
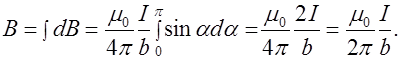 (6.6)
(6.6)
Линии индукции магнитного поля - касательные к вектору 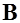 индукции в каждой точке. Для прямолинейного провода с током эти линии представляют собой концентрические окружности, охватывающие провод, как показано на рис. 6.5. Плоскости окружностей перпендикулярны к проводу.
индукции в каждой точке. Для прямолинейного провода с током эти линии представляют собой концентрические окружности, охватывающие провод, как показано на рис. 6.5. Плоскости окружностей перпендикулярны к проводу.
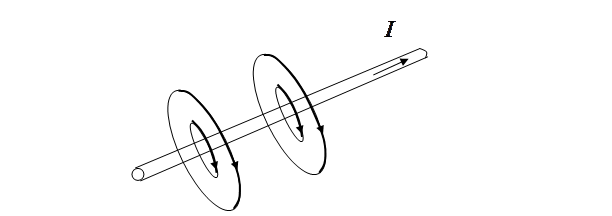
Рис. 6.5. Линии индукции магнитного поля прямолинейного провода с током
Направление обхода линий индукции задается вектором 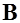 индукции магнитного поля. Это направление связано с направлением тока в проводе по правилу правого винта, как видно из рис. 6.5.
индукции магнитного поля. Это направление связано с направлением тока в проводе по правилу правого винта, как видно из рис. 6.5.
Применение принципа суперпозиции и формулы (6.4) позволяет найти индукцию магнитного поля, создаваемого постоянным током силой 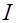 , который течет по замкнутому контуру
, который течет по замкнутому контуру 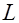 :
:
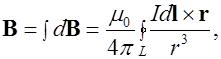 (6.7)
(6.7)
где 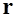 - радиус-вектор, проведенный от элемента тока
- радиус-вектор, проведенный от элемента тока 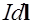 к точке наблюдения, где вычисляется вектор
к точке наблюдения, где вычисляется вектор 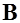 .
.
Формула (6.7) применима для линейного тока. Пусть постоянный ток распределен в объеме 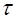 с плотностью
с плотностью 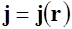 . Переход от линейного тока к объемному току поясняет рис. 6.6, где показан элемент тонкого проводника длиной
. Переход от линейного тока к объемному току поясняет рис. 6.6, где показан элемент тонкого проводника длиной 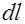 и поперечным сечением
и поперечным сечением 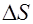 .
.

Рис. 6.6.
Объем элемента равен 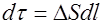 . Связь силы тока с плотностью тока в проводнике дается формулой
. Связь силы тока с плотностью тока в проводнике дается формулой 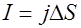 , откуда
, откуда 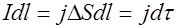 , или в векторном виде
, или в векторном виде
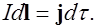 (6.8)
(6.8)
С учетом (6.8) из (6.7) выражаем индукцию магнитного поля, созданного объемными токами, распределенными в объеме 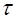 как
как
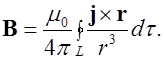 (6.9)
(6.9)
 2014-02-10
2014-02-10 20617
20617








