Алгоритмы поиска локальных экстремумов на изображениях

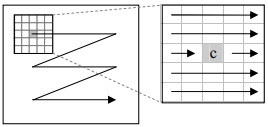
Прямой подход к поиску экстремумов в двухмерном массиве представлен на рис. 1, а. Пиксели исходного изображения анализируются в порядке растрового сканирования (слева направо, затем сверху вниз). Каждый анализируемый пиксель сравнивается с другими пикселями в своей окрестности размером 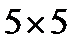 пикселей также в порядке растрового сканирования [9]. Центральный пиксель С не является максимальным, если найден любой более значимый или равный соседний пиксель. Затем алгоритм переходит к следующему пикселю в строке сканирования. Прямой подход требует  сравнений на пиксель для 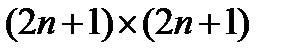-окрестности. Наилучшему варианту сооветствует ситуация, когда вектор интенсивности меняется на противоположный. При этом прямой подход требует только одного сравнения на пиксель. В среднем, однако, данный подход требует  сравнений на пиксель.

а	б	в

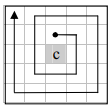
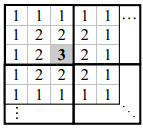
Рис. 1. Представление способов сканирования изображений: а – растровое сканирование;
б – спиральное сканирование; в – Block partitioning

Cложность алгоритма растрового сканирования может быть значительно уменьшена путем анализа соседних пикселей в другом порядке. В работе [10] представлен такой алгоритм с локальным спиральным порядком (рис. 1, б). Сначала, в результате сравнения, центральный пиксель, возможно, будет локальным максимумом в 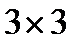-окрестности. Затем он проверяется
в большей окрестности. Так как количество локальных максимумов в 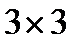-окрестности
в изображении обычно невелико (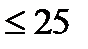 % от общего количества пикселей), алгоритм спирального порядка быстро находит любые немаксимальные значения, пропускает
их и переходит на следующий пиксель. Число локальных максимумов в окрестности с размером 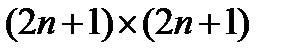 пикселей также быстро уменьшается, поскольку размер окрестности увеличивается. В результате вычислительная сложность этого алгоритма примерно постоянна (не более  сравнений на пиксель для обнаружения в 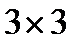-окрестности немаксимальных пикселов) независимо от размера окрестности.

В работе [9] представлен эффективный алгоритм NMS, который требует 2,39 сравнений на пиксель в среднем и 4 сравнения на пиксель в худшем случае. Они отметили, что максимальный пиксель в окрестности размером 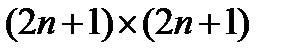 пикселя также является максимальным для любого окна размером 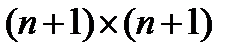пикселей. Входное изображение разбивается на неперекрывающиеся блоки размера  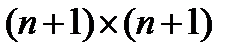пикселей и локальный максимум каждого блока детектируется (рис. 1, в иллюстрирует это для ). Затем
для максимального размера блока 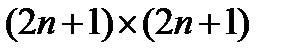 пикселей за исключением охватывающего блока  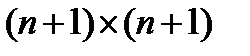пикселей. Используя только одно сравнение на пиксель, шаг разбиения блока уменьшает количество локальных максимумов с фактором 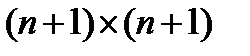. В результате метод достаточно эффективен для больших размеров окрестностей. Решение уменьшить количество дополнительных сравнений на одного кандидата до ,
значительно увеличивает сложность алгоритма и использование памяти.

Метод NMS для окрестности 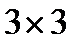 пикселей часто решается с помощью математической морфологии [11, 12], в результате чего входное изображение сравнивается с его дилатацией серого цвета. Пиксели, где два изображения равны, соответствуют локальным максимумам. Однако математическая морфология не возвращает строгие локальные максимумы,
где центральный пиксель строго больше, чем все соседние пиксели. С точки зрения вычислительной сложности морфология также неэффективна – реализация дилатации для
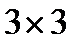-окрестности полутонового изображения требует шести сравнений на пиксель [6, 7].

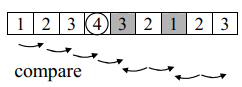
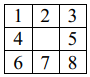
В [13] предложен алгоритм 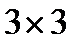 сканирующей линии для NMS, который требует не более 2 сравнений на пиксель. Алгоритм сначала ищет одномерные локальные максимумы вдоль линии сканирования. Затем каждый максимальный уровень сканирования сравнивается с соседними пикселями в соседних строках. Две двоичные маски сохраняются для текущей и следующей строк сканирования в буфере. По мере обработки нового центрального пикселя соседние ему пиксели маскируются, если они меньше центрального пикселя. Маскированные пиксели будут пропущены, когда наступит их очередь обработки (рис. 2). В результате этот алгоритм NMS
для окрестности 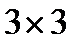 пикселей требует не более двух сравнений на пиксель.

а	б	в

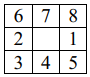
Рис. 2. Маски сканирующей линии 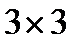 – окрестности: а – 1-D Non-maximum Suppression [13];

б – растровое сканирование; в – Scan-line [13]

Алгоритм сканирующей линии для 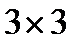 -окрестности может быть расширен до блоков 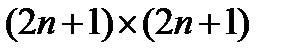пикселей при  [13]. Предположим, что максимумы 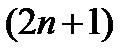-окрестности на текущей линии сканирования расположены так, как показано на рис. 3, б (пиксели
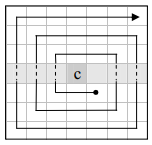
в окружностях). Эти 1-D максимумы служат кандидатами на двумерные максимумы. Каждый кандидат проверяется на экстремум в 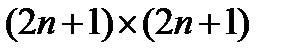-окрестности в спиральном порядке, аналогичном методу Forstner [10]. При этом соседние пиксели, расположенные на одной линии сканирования, уже были сопоставлены и потому могут быть пропущены (серые пиксели
на рис. 3, в). Это приводит к тому, что максимум для -соседей сравнивается с каждым кандидатом. В результате среднее количество сравнений на один кандидат намного меньше благодаря порядку перемещения по спирали.

а	б	в

Рис. 3. Сканирующий алгоритм NMS для 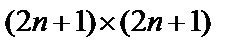-окрестности ():
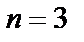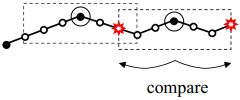
  а – 1-D обнаружение пиков; б – 1-D исключение не-максимумов; в – спиральное сканирование

Обнаружение максимумов в 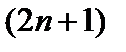 – окрестности на одномерной сканирующей линии функции  подробно показано на рис.3 а. Если 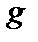 – знак конечной разности функции 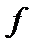, значение 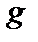равно либо –1, 0 или 1 в зависимости от локального наклона . Cледовательно, rонечная разность 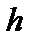, равна –2 на локальных пиках, +2 в локальных желобах и 0 в другом месте. Таким образом, для обнаружения 1-D пика и минимума требуется только одно сравнение
на пиксель. Затем каждый 1-D экстремум сравнивается с его участком в 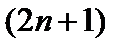 – окрестности со знанием экстремума детектора 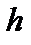. Соседние пиксели, которые находятся на последовательном склоне вниз от локального пика, т. е.  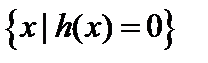, по определению меньше, чем текущий пик, поэтому их не нужно повторно сравнивать. Пиксели, расположенные вне закрывающих впадин текущего пика, требуются дополнительного сравнения. Число дополнительных сравнений для получения максимумов 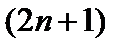-окрестности из исходного списка максимумов -окрестности очень мало для гладкой функции .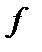

Недостатками рассмотренных выше алгоритмов являются низкая скорость поиска, наличие ошибок обнаружения экстремумов на границах блоков изображения, пропуск локальных минимумов. В этой связи актуальной является задача поиска всех локальные однопиксельных экстремумов (как максимумов, так и минимумов) на изображении с низкой вычислительной сложностью без использования дополнительной памяти. Предлагаемый алгоритм позволяет быстро найти все локальные однопиксельные экстремумы.