Мы рассмотрели работу АЦП как устройства, преобразующего аналоговый сигнал в цифровой. Показали, что при подаче на вход АЦП аналогового гармонического сигнала на его выходе появляется цифровая синусоида с теми же значениями частоты и фазы, какие были в исходном аналоговом сигнале. А теперь посмотрим, что образуется на выходе АЦП, если из устройства цифровой обработки сигналов (см. рис. 1.1) исключить ограничивающий фильтр ОФ, и на вход АЦП подать гармоническое колебание, частота которого превосходит верхнюю границу интервала Найквиста.
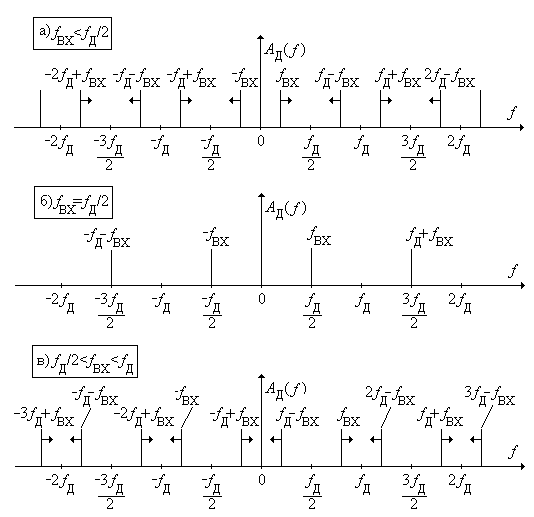
Рис. 1.7.
Спектр сигнала на выходе АЦП при вариации f ВХ.
Итак, пусть на входе АЦП действует синусоидальное колебание u (t) = sin2p f ВХ t. Рассмотрим спектр на выходе АЦП при разных соотношениях между значениями f ВХ и частотой дискретизации f Д.
а) Частота входного колебания меньше значения верхней границы интервала Найквиста: f ВХ < f Д/2.
Спектр дискретизированного колебания A Д(f)для этого случая представлен на рис. 1.7,а. При увеличении частоты колебания основная спектральная линия f ВХ и все ее копии перемещаются в направлениях, показанных стрелками. Линия f ВХ, соответствующая спектру исходного аналогового колебания, остается в пределах интервала Найквиста. Будем считать, что цифро-аналоговый преобразователь ЦАП совместно с формирующим фильтром ФФ выполняют функцию идеального ФНЧ, верхняя граничная частота которого равна f Д/2. Тогда на выходе ФФ будет восстановлено преобразованное синусоидальное колебание, частота которого f ВЫХ в точности равна частоте f ВХ входного синусоидального колебания. Зависимость f ВЫХ от f ВХ представляет собой прямую, выходящую из начала координат под углом 45о (участок 0 на рис. 1.8).
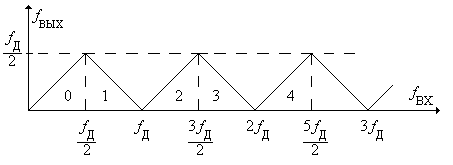
Рис. 1.8.
Частотно-преобразующая функция АЦП.
б) Частота входного колебания равна значению верхней границы интервала Найквиста: f ВХ = f Д/2.
Спектр дискретизированного колебания представлен на рис. 1.7,б. Значение частоты восстановленного колебания на выходе опять равно значению частоты входного колебания, т.е. f Д/2 (рис. 1.8).
Отметим, что если исходное синусоидальное колебание имеет частоту f Д/2, то его восстановление возможно только в том случае, когда отсчетные импульсы не попадают на нулевые значения колебания. Такое положение может быть обеспечено только при жесткой синхронизации последовательности отсчетных импульсов относительно фазы входного колебания.
в) Частота входного колебания меняется в пределах f Д/2 < f ВХ < f Д.
В этом случае спектральная линия колебания выходит из интервала Найквиста, а в интервал Найквиста попадает составляющая с частотой f Д – f ВХ, как показано на рис. 1.7,в. На выходе формирующего фильтра восстанавливается синусоидальное колебание с этой частотой. При стремлении значения частоты f ВХ к значению частоты f Д частота восстановленного колебания уменьшается до нуля (участок 1 на рис. 1.8).
Дальнейшее увеличение частоты f ВХ приводит к повторению зависимости f ВЫХ от f ВХ (участки 2, 3 и т.д.). Здесь АЦП работает как своего рода преобразователь частоты, уменьшая частоту входного гармонического колебания до значения, которое находится в пределах главного интервала частот 0 ÷ f Д/2.
Определим частоту f ВЫХ преобразованного колебания, используя график f ВЫХ = j(f ВХ), показанный на рис. 1.8. График представляет собой бесконечную последовательность пронумерованных участков протяженностью D f = f Д/2. Номера участков начинаются с нуля: N = = 0, 1, 2, … Введем вспомогательную величину A: A = f ВХ/D f = 2 f ВХ/ f Д. В общем случае A является числом с целой Ц и дробной Д частью:
A = 2 f ВХ/ f Д = Ц + Д.
Значение Ц определяет номер участка, на котором находится отсчет f ВЫХ: N = Ц. Если N - четное, т.е. N = 0, 2,..., то f ВЫХ = (f Д/2)· Д. Если N - нечетное, то f ВЫХ = (f Д/2)·(1 - Д).
Пример. На входе АЦП действует гармоническое колебание с частотой f ВХ = 91,32 кГц. Частота дискретизации f Д = 24 кГц. Определить значение f ВЫХ.
Решение. Найдем A: A = 2 f ВХ/ f Д = 2·91,32/24 = 7,61 = 7 + 0,61. Поскольку N - нечетное, то f ВЫХ = (f Д/2)·(1 - Д) = 12 кГц·0,39 = 4,68 кГц.
Приведем еще один пример, иллюстрирующий изложенный материал. Пусть на входе АЦП действует колебание s 1(t) с частотой f 1 = = 900 Гц: s 1(t) = sin(2p f 1 t) = sin(2p·900· t). Установим значение частоты дискретизации f Д = 1000 Гц. Найдем A:
A = 2 f ВХ/ f Д = 2·900 Гц/1000 Гц = 1,8 = 1 + 0,8.
Здесь также как и выше, N = Ц = 1, т.е. является нечетным числом, следовательно,
f ВЫХ = (f Д/2)·(1 - Д) = 500 Гц·(1 - 0,8) = 100 Гц.
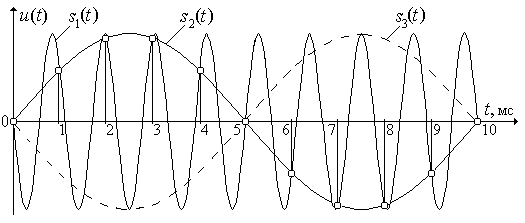
Рис. 1.9.
Эффект наложения колебаний.
На рис. 1.9 приведена эпюра колебания s 1(t) с частотой 900 Гц, там же показаны отсчетные импульсы (столбики с квадратиками), следующие с периодом 1 мс (частота дискретизации 1 кГц). На этом же рисунке изображена эпюра колебания s 2(t) с частотой 100 Гц. Очевидно, что выборки колебания s 1(t) являются также выборками низкочастотного колебания s 2(t), частота которого попадает в интервал Найквиста, поэтому на выходе формирующего фильтра восстанавливается колебание s 2(t). Это колебание является помехой, так как его не было в исходном аналоговом сигнале. Появление помехи связано с отключением ограничивающего фильтра ОФ, поэтому уместно еще раз отметить его значение для подавления помех.
Попадая в интервал Найквиста, колебание s 2(t) может вызывать также эффект наложения колебаний, если в исходном сигнале наряду с колебанием s 1(t) было колебание s 3(t) (пунктир на рис. 1.9) с частотой, равной частоте колебания s 2(t). Результат наложения колебаний s 2(t) и s 3(t) зависит от разности фаз между этими колебаниями. На рис. 1.9 показан случай, когда эта разность фаз равна 180о, что может привести к полной компенсации колебания s 3(t), если амплитуды колебаний s 2(t) и s 3(t) равны.
Преобразование частоты колебаний в АЦП приводит, как показано выше, к отрицательным эффектам, устранить которые можно, только включив ограничивающий фильтр на входе устройства обработки сигналов. В то же время само явление преобразования частоты колебаний в АЦП представляет интерес и может быть использовано на практике.
 2021-11-13
2021-11-13 293
293








