Контрольные вопросы. Глава 3. Способы описания цифровых фильтров. Z-преобразование

Контрольные вопросы

1. Что такое разностное уравнение? Как его получить из дифференциального уравнения линейного фильтра?

2. Запишите разностное уравнение для цифрового фильтра, аналогом-прототипом которого является интегрирующая RC -цепь. Изобразите структурную схему фильтра.

3. Дайте определение рекурсивного и нерекурсивного фильтра. Приведите примеры таких фильтров.

4. Что такое КИХ- и БИХ-фильтры?

5. Дайте сравнительную характеристику КИХ- и БИХ-фильтров.

6. Что такое амплитудно-частотная и фазочастотная характеристики цифрового фильтра? Какова их связь с комплексным коэффициентом передачи фильтра?

7. Почему АЧХ цифрового фильтра периодична по частоте?

8. Что такое «наложение АЧХ цифровых фильтров»?

Глава 3. СПОСОБЫ ОПИСАНИЯ ЦИФРОВЫХ ФИЛЬТРОВ

3.1.Z-преобразование

Одним из результативных и широко распространенных направлений в исследовании аналоговых линейных систем (в том числе радиотехнических) является операторный метод, базирующийся на известном преобразовании Лапласа:

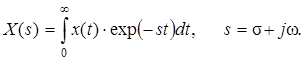                                         (3.1)

Преобразование (3.1) позволяет осуществить перевод ориги­нала x (t)из области непрерывного времени t в его изобра­жение X (s)в комплексной s -области.

В области дискретного времени преобразование Лапласа последовательности x (n) принимает вид

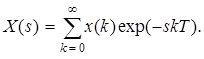                                                             (3.2)

При переходе от (3.1) к (3.2) опущена постоянная величина T, аналогично тому, как это было сделано при выводе выражения (2.2).

Трансцендентность изображений дискретных последовательностей из-за наличия экспоненты в (3.2) приводит к оп­ределенным трудностям при анализе. Поэтому применительно к дискретным и цифровым устройствам используют не дискретное преобразование Лапласа, а так называемое z -преобразование, которое получается из (3.2) заменой: exp(sT) = z:

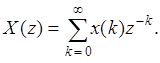                                                                   (3.3)

В Приложении 2 приведены выражения для z -преобразования различных типовых последовательностей.

Рассмотрим некоторые важные свойства z -преобразования.

1. Линейность. Если X ₁(z)и Х ₂(z)являются z -преобразованиями последовательностей х ₁(п)и x ₂(n),то при любых действительных а и b z -преобразование последовательности ax ₁(n) +bx ₂(n)равно аХ ₁(z)+ bХ ₂(z).Это свойство - подтверждение принципа суперпозиции, и оно непосредственно вытекает из опре­деления z -преобразования (3.3).

2. Задержка. Рассмотрим две последовательности: исходную х (п)(рис. 3.1а) и последовательность y (n) = x (n - m), которая получена путем задержки   х (п) на m тактов (рис. 3.1б, он соответствует задержке на m = 2 такта). Пусть известно z -преобразование X (z)последовательности х (п). Тогда z -преобразование последова­тельности y (n) равно: Y (z) = z ^{- m}X (z).

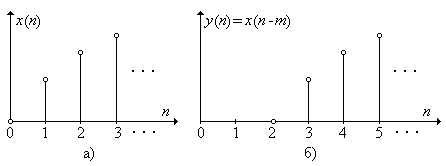
Рис. 3.1.

Исходная - а) и задержанная - б) последовательности отсчетов.

 

 Докажем это утверждение. Найдем z -преобразование последовательности y (n), используя выражение (3.3):

                

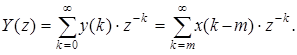
Произведем замену переменных: n = k - m. Для Y (z) получим тогда следующее выражение:

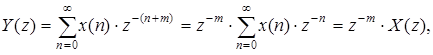                   (3.4)                 

что и требовалось доказать.

Из последнего выражения следует, в частности, что множитель z^±m должен рассматриваться как оператор сдвига преобразуемой последовательности на m тактов дискретиза­ции. Знак показателя определяет направление сдвига (минус - задержка, плюс - опережение).

3. Свертка. Если последовательности х (п)соответствует z -пре­об­разова­ние X (z),а последовательности y (п) - z -преобразование Y (z),то дискретной свертке этих последовательностей    

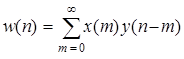                                                           (3.5)

соответствует произведение их z -преобразований:

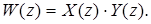                                                                 (3.6)

Докажем справедливость соотношения (3.6). Используя (3.3) и (3.5), составим исходное выражение для z -преобразования последовательности w (n):

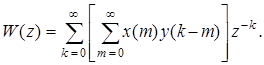                                                    (3.7)

Изменим в (3.7) порядок суммирования:

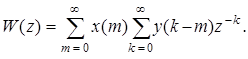                                                       (3.8)

 Внутренняя сумма в (3.8) представляет собой z -преобразование последовательности y (n), задержанной на m тактов дискретизации, т.е. 

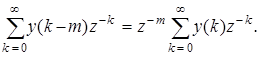                                                    (3.9)

Подставив (3.9) в (3.8), получим произведение независимых сумм:

                

Таким образом, выражение (3.6) доказано.

4. Обратное z-преобразование ставит в соответствие функции комплексной переменной X (z) последовательность x (n). Это соответствие выражается формулой:

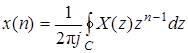                         ,                            (3.10)

где C - контур, расположенный в области сходимости подынтегрального выражения X (z)× z^{n- 1} и охватывающий начало координат в z -плос­ко­сти. С помощью обратного z -преобразования можно определить ДИХ h (n) по известной передаточной функции фильтра H (z) и решать другие задачи. Способы вычисления интеграла в (3.10) рассмотрены в Приложении 3.