Разностное уравнение цифрового фильтра

Выберем в качестве аналогового фильтра-прототипа прос­тейший вариант - фильтр нижних частот, состоящий из од­нозвенной интегрирующей RC -цепи (рис. 2.1).

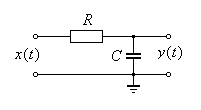
Рис. 2.1.

Аналог-прототип - RC -цепь.

 

Получение эквивалентного цифрового фильтра, обладающего свойствами аналогового прототипа, базируется в проводимом ниже рассмотрении на операции дискретиза­ции временных процессов, действующих в цепях этого прото­типа: входного x (t) и выходного y (t) эффектов, импульсной и переходной характеристик. При дискретизации временных процессов производная по времени заменяется выражением:

 

 

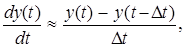                                                       (2.3)

где D t – приращение по времени.

В цифровых фильтрах D t равно интервалу дискретизации T; y (t – D t) и y (t) – значения y в дискретные моменты (n – 1) T и nT, где n – номер интервала дискретизации. С учетом этого производную в (2.3) можно представить в виде:

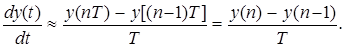                               (2.4)

Дифференциальное уравнение фильтра в виде однозвенной RC -цепи (рис.2.1) имеет вид:

                                                    

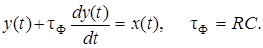
Заменим y (t) на y (n), x (t) на x (n), а производную представим в соответствии с выражением (2.4). В результате получим:

                      у (п) = ах (п) + bу (п - 1),                                      (2.5)

где

                   

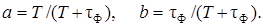
Уравнение (2.5) носит название разностного уравнения. Ценность разностного уравнения состоит в том, что оно поз­воляет сразу же, без каких-либо дополнительных исследова­ний, представить структуру цифрового фильтра. Действитель­но, в соответствии с (2.5) выходная последовательность у (п)является суммой двух последовательностей, определяемых первым и вторым слагаемыми правой части (2.5). Следова­тельно, выход цифрового фильтра должен быть соединен с выходом двухвходового сумматора. На первый вход сумматора поступает входная последовательность х (п),предвари­тельно умноженная на постоянную величину а,а на второй вход – выходная последовательность у (п – 1), задержанная на один такт дискретизации и умноженная на вторую по­стоянную величину b.

Структура полученного цифрового фильтра показана на рис. 2.2. Назовем этот фильтр цифровой RC-цепью.

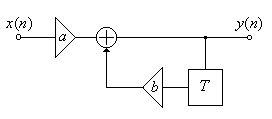
Рис. 2.2.

Структура цифровой RC -цепи.

Заметим, что цифровая RC- цепь состоит из комбинации всего лишь трех типов функциональных блоков, выполняющих операции суммирования, умножения и задержки на один такт T. В дальнейшем мы увидим, что наличие таких функциональных блоков присуще цифровым фильтрам сколь угодно сложной структуры. Величины а и b называются коэффициентами цифрового фильтра.

Особенностью структурной схемы полученного цифрового фильтра является наличие петли обратной связи с выхода на вход сумматора, состоящей из блока задержки и умножителя на коэффициент b. Дейст­вие обратной связи заключается в том, что в вычислении очередного отсчета выходной последовательности у (п)участ­вует ее предыдущий отсчет у (п -1). Цифровые фильтры та­кого типа называются рекурсивными.

Убедимся теперь, что цифровой фильтр с разност­ным уравнением (2.5) действительно соответствует заданно­му фильтру-прототипу в виде интегрирующей RC- цепи. Проверку на такое соответствие про­ведем, сравнив импульсные характеристики полученного циф­рового фильтра и его аналогового прототипа.

Для фильтра в виде интегрирующей RC -цепи (рис. 2.1) импульсная ха­рактеристика, т. е. отклик на единичный d-импульс, описы­вается экспонентой:

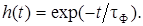                                                                           (2.6)

После дискретизации этой функции образуется так называе­мая дискретная импульсная характеристика (ДИХ), имеющая вид:

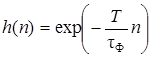                              .                                     (2.7)

Вполне естественно ожидать, что такой характеристикой об­ладает синтезированный цифровой фильтр, описываемый разност­ным уравнением (2.5). Проверим это. Для этого на вход цифрового фильтра, как и в аналоговом варианте, необходимо подать испытательное воз­действие в виде цифрового единичного импульса (1.2). Выходной эффект y (n) = h (n), т.е.саму ДИХ, рассчитаем с помощью разностного уравнения (2.5). Результаты такого расчета приведены в табл. 2.1.

Таблица 2.1.

n	x (n)	y (n - 1)	y (n)
			a
		a	ab
		ab	ab 2
		ab 2	ab 3
		ab 3	ab 4
...	...	...	...

 

При составлении табл. 2.1 предполагалось, что в момент подачи единичного импульса (момент нулевой выборки n = 0) фильтр был «разряжен», т.е. предыдущее значение у (-1) = 0. Таким образом, в соответствии с выражением (2.5) ДИХ исследуемого цифро­вого фильтра имеет вид

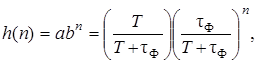                                                  (2.8)

что отличается от экспоненты (2.7). Преобразуем (2.8), имея в виду два обстоятельства:

коэффициент а устанавливает только масштаб выходной последовательности и его выбор может быть в достаточной мере произвольным, примем а =1;

коэффициент b представим так:

                                      

         

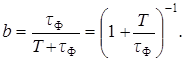
Легко видеть, что выражение в скобках – это первые два члена ряда, представляющего экспоненту

                             

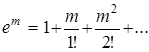
при малых m, т.е. небольших значениях отношения T /t_Ф.

С учетом отмеченных обстоятельств выражение (2.8) можно представить в виде:

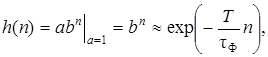                                                (2.9)

что, хотя и приближенно, но соответствует требуемой ДИХ (2.7) нашего фильтра-прототипа.

Точное соответствие между ДИХ цифрового фильтра по рис. 2.2 и импульсной характеристикой фильтра-прототипа по рис. 2.1 будет иметь место при следующих коэффициентах:

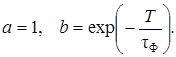                                                                (2.10)

Как мы показали, описанный здесь метод дискретизации дифференциального уравнения фильтра-прототипа не позволяет точно опре­делить коэффициенты цифрового фильтра. Причины этого, а также другие более точные методы дискретизации будут рассмотрены позже (раздел 6.2).

В заключение укажем, что ДИХ, описываемая выражениями (2.8) или (2.9), имеет теоретически бесконечную протяженность во времени. Фильтры с такой ДИХ называются БИХ-фильтрами.