После опыта Эрстеда началось интенсивное изучение магнитных полей, создаваемых проводниками различной формы. Пришли к выводу, что магнитная индукция проводника с током пропорциональна силе тока, зависит от формы и размеров проводника, а также от расположения рассматриваемой точки по отношению к проводнику.
Элемент проводника с током 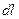 создает в некоторой точке
создает в некоторой точке 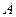 индукцию поля
индукцию поля 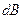 , равную
, равную
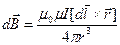 . (1)
. (1)
Направление 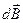 перпендикулярно
перпендикулярно 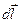 и
и 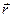 , то есть перпендикулярны плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции.
, то есть перпендикулярны плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции.
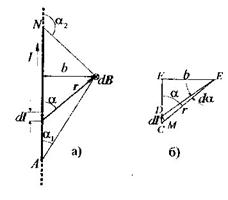
 | По правилу правого винта направление головки дает направление 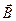 . Модуль вектора . Модуль вектора 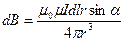 = = 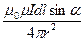 . (2) Для магнитного поля справедлив принцип суперпозиции. Магнитное поле создаваемое несколькими токами или движущимися зарядами равно векторной сумме магнитных полей, создаваемых каждым током в отдельности . (2) Для магнитного поля справедлив принцип суперпозиции. Магнитное поле создаваемое несколькими токами или движущимися зарядами равно векторной сумме магнитных полей, создаваемых каждым током в отдельности 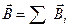 = = 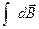 (3) (3) |
| Рис. 6. |
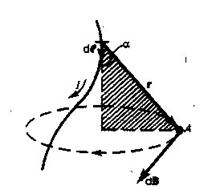
Теорема Био-Савара-Лапласа позволяет определить поле любого тока. Применим формулу (3) для вычисления поля, создаваемого отрезком провода.
Вычислим магнитное поле, создаваемое отрезком проводника AN с током 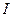 , в точке, отстоящей от проводника на расстоянии
, в точке, отстоящей от проводника на расстоянии 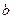 (рис.7). Разобьем мысленно проводник с током на элементы тока
(рис.7). Разобьем мысленно проводник с током на элементы тока 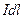 . Векторы
. Векторы 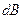 от всех элементов тока совпадают по направлению и направлены от нас. Поэтому векторное интегрирование (3) можно заменить скалярным, используя выражение
от всех элементов тока совпадают по направлению и направлены от нас. Поэтому векторное интегрирование (3) можно заменить скалярным, используя выражение
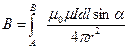 .
.
(2) | Выразим 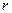 и и 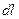 через угол через угол 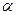 (рис.7б). Из (рис.7б). Из 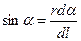 следует, что следует, что 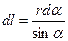 . . 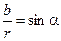 дает дает 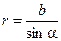 и и 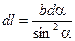 . . |
| Рис.7. |
Теперь
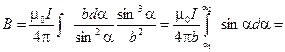
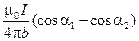 (4)
(4)
Для бесконечного проводника  и
и
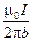 (5).
(5).
Магнитное поле, создаваемое круговым током.
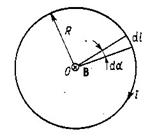 | 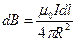 , , 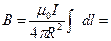 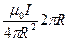 = = 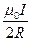 . . 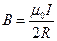 |
| Рис.8. |
 2014-02-13
2014-02-13 2023
2023
