И площадь агломерации производств. Агломерируемые производства должны размещаться в штрихованном сегменте

Агломерируемые производства должны размещаться в штрихованном сегменте. Выбор точки размещения происходит с учетом транспортного фактора. В более общем случае несколько предприятий образуют не один, а несколько сегментов.

А. Вебер рассматривает различные ситуации при осуществлении агломерации, конкретизируя методику нахождения штандорта. Он предлагает формулы агломерационных эффектов.

Пусть М — производственная масса какого-либо крупного производства. Величина сбережений от агломерации в расчете на единицу продукта будет выражаться в виде функции сбережения — f(M). Тогда общая величина сбережений на всю производственную массу составит:

Э₁ = М • f(M).

Допустим, что с крупным производством сливается мелкое производство с производственной массой т. Тогда общая суммасбережения для двух производств составит:

Э₂ = (М + т) • f(M + т).

Определим приращение сбережения, получаемого в результате слияния двух производств:

Э = Э₂ − Э_{1 =} (М + т) • f(M + т) − M • f (M)

Cлияние мелкого производства с крупным происходит, согласно А. Веберу, в том случае, если величина сбережения от слияния предприятий больше (или по крайней мере не меньше) перерасхода транспортных затрат из-за переноса производства т в пункт производства М, т.е.:

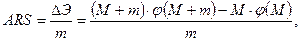
где А — штандортный вес;

R — радиус отклонения;

S —ставка транспортного тарифа (т/км)

Отсюда можно определить величину наибольшего, экономи­ки допустимого, радиуса отклонения.

Определяем первую производную функции:

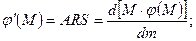
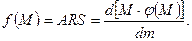
«Функция f(M), называемая функцией агломерации, служит выражением притягательной силы крупного производства по отношению к рассеянным мелким производствам. Поскольку f (M) = ARS, то R = f (M): AS, т.е. максимально допустимый радиус отклонения прямо пропорционален функции агломерации и обратно пропорционален штандортному весу и тарифной ставке.

Выведенная формула агломерации f(M) = ARS включает три фактора, от которых зависит агломерация. Требуется учесть еще одно условие — производственную плотность.

Обозначим через р производственную плотность, под которой здесь понимается объем продукции, приходящейся на единицу площади с радиусом R, при равномерном распределении производства на данной площади. Тогда вся производственная масса, притягиваемая к агломерационному центру, будет равна πR²p = М.

Отсюда

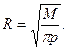
Сравнивая полученную формулу с ранее выведенной, получаем окончательную формулу агломерации

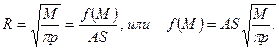
А. Веберу первому удалось выработать многофакторную теорию размещения промышленного предприятия, опирающуюся на методы количественного анализа (математическое моделирова­ние). Так же как и его предшественник В. Лаунхардт, А. Вебер не вышел за рамки проблемы размещения отдельного предприятия. Однако его исследования стали мощным стимулом для создания более общих теорий размещения.