| Простые импли-канты | Конституенты единицы | |||||
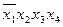 | 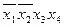 | 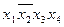 | 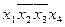 | 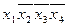 | 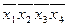 | |
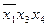 | X | X | ||||
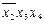 | X | X | ||||
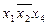 | X | X | ||||
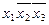 | X | X | ||||
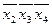 | X | X |
Для каждой импликанты найдем конституенты единицы, которые ею поглощаются, т. е. те конституенты, собственной частью которых является данная импликанта. Например, импликанта 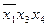 поглощает конституенты
поглощает конституенты 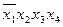 и
и 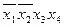 , импликанта
, импликанта 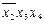 — конституенты
— конституенты 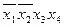 и
и 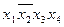 и т. д. Клетки импликантной матрицы, образованные пересечением строк с импликантами и колонок с поглощаемыми ими конституентами, отметим какими-либо символами..
и т. д. Клетки импликантной матрицы, образованные пересечением строк с импликантами и колонок с поглощаемыми ими конституентами, отметим какими-либо символами..
Чтобы получить минимальную дизъюнктивную нормальную форму заданной функции, достаточно найти минимальное число импликант, которые совместно накрывают крестиками все колонки импликантной матрицы.
Из табл. 2.3.1 следует, что в минимальную форму обязательно должны войти импликанты 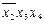 и
и 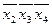 , так как только они накрывают крестиками первую и шестую колонки импликантной матрицы.
, так как только они накрывают крестиками первую и шестую колонки импликантной матрицы.
Кроме того, имлликанта 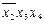 накрывает вторую, а импликанта
накрывает вторую, а импликанта 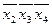 — пятую колонки. Поэтому остается накрыть только третью и четвертую колонки. Для этого можно выбрать пары импликант:
— пятую колонки. Поэтому остается накрыть только третью и четвертую колонки. Для этого можно выбрать пары импликант: 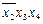 и
и 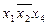 ;
; 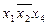 и
и 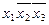 или одну импликанту
или одну импликанту 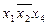 . Если выбрать указанные выше пары импликант, то импликанты
. Если выбрать указанные выше пары импликант, то импликанты 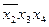 и
и 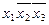 оказываются лишними, так как импликанта
оказываются лишними, так как импликанта 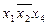 одна накрывает третью и четвертую колонки таблицы. Таким образом, выбрав импликанту
одна накрывает третью и четвертую колонки таблицы. Таким образом, выбрав импликанту 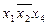 , получим минимальную дизъюнктивную нормальную форму заданной функции.
, получим минимальную дизъюнктивную нормальную форму заданной функции.
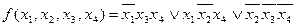 ,
,
которая совпадает с первой тупиковой формой. Если дополнительно к 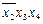 и
и 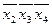 выбрать импликанты
выбрать импликанты 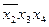 и
и 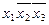 , то лишних импликант не оказывается, а полученное выражение
, то лишних импликант не оказывается, а полученное выражение
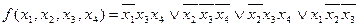 ,
,
является второй тупиковой формой заданной функции.
Пример. Найти минимальные формы переключательной функции
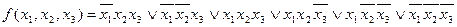 . (2.3.1)
. (2.3.1)
Проводя все операции склеивания и поглощения, получим сокращенную дизъюнктивную нормальную форму:
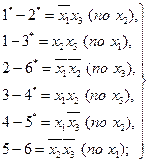 (2.3.2)
(2.3.2)
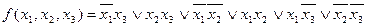 . (2.3.3)
. (2.3.3)
Составим импликаитную матрицу (табл. 2.3.2), выписав из выражения (2.3.1) все конституенты единицы, а из выражения (2.3.3) - все простые импликанты. При заполнении импликантной матрицы удобно пользоваться формой записи (2.3.2): следует поставить крестики в тех колонках, номера которых совпадают с числами, стоящими в левой части формы (2.3.2).
Таблица 2.3.2
Импликантная матрица
| Простые импли-канты | Конституенты единицы | |||||
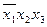 | 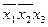 | 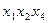 | 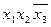 | 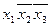 |  | |
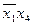 | X | X | ||||
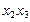 | X | X | ||||
 | X | X | ||||
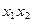 | X | X | ||||
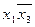 | X | X | ||||
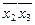 | X | X |
Для импликанты 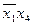 крестиками отмечаются первая и вторая колонки; для
крестиками отмечаются первая и вторая колонки; для 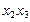 — первая и третья и т. д. Заметим, что каждая колонка табл. 2.3.2 отмечена двумя крестиками. Поэтому из выражения (2.3.3) можно исключить любую импликанту. Минимальное количество импликант, накрывающих крестиками все колонки, равно трем:
— первая и третья и т. д. Заметим, что каждая колонка табл. 2.3.2 отмечена двумя крестиками. Поэтому из выражения (2.3.3) можно исключить любую импликанту. Минимальное количество импликант, накрывающих крестиками все колонки, равно трем:
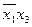 накрывает первую и вторую колонки,
накрывает первую и вторую колонки,
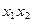 накрывает третью и четвертую колонки,
накрывает третью и четвертую колонки,
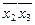 накрывает пятую и шестую колонки.
накрывает пятую и шестую колонки.
Поэтому минимальная дизъюнктивная нормальная форма заданной функции имеет вид
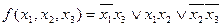 .
.
Можно накрыть все колонки табл. 3.9 и другими импликантами:
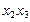 накрывает первую и третью колонки,
накрывает первую и третью колонки,
 накрывает вторую и шестую колонки,
накрывает вторую и шестую колонки,
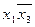 накрывает четвертую и пятую колонки.
накрывает четвертую и пятую колонки.
Таким образом, данная функция имеет вторую минимальную форму
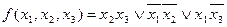 .
.
Переключательная функция 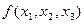 имеет несколько других тупиковых форм, которые, однако, не являются минимальными. Например, тупиковыми будут следующие формы:
имеет несколько других тупиковых форм, которые, однако, не являются минимальными. Например, тупиковыми будут следующие формы:
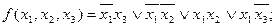
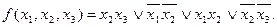
На основании изложенного сформулируем алгоритм получения минимальных дизъюнктивных нормальных форм переключательной функции.
1. Переключательную функцию представляют в совершенной дизъюнктивной нормальной форме. При этом, если функция задана таблицей, то ее следует записать «по единицам»; если же функция задана в произвольной аналитической форме, то совершенную дизъюнктивную нормальную форму можно получить, применяя операции развертывания, правила де Моргана и другие формулы булевой алгебры.
2. В полученной совершенной дизъюнктивной нормальной форме проводят все операции неполного склеивания и поглощения. В результате этого получается сокращенная дизъюнктивная нормальная форма заданной функции.
3. Находят минимальные дизъюнктивные нормальные формы по импликантной матрице. Если количество импликант в сокращенной дизъюнктивной нормальной форме невелико, то можно найти тупиковые формы методом испытания импликант и выбрать среди них минимальные.
Заметим, что в ряде случаев минимальная дизъюнктивная форма совпадает с сокращенной. Например, сокращенная дизъюнктивная нормальная форма любой переключательной функции двух аргументов совпадает с минимальной формой. Точно так же импликантные матрицы применяются для получения тупиковых и минимальных конъюнктивных нормальных форм переключательных функций.
2.4. Метод испытания импликант
Этот метод удобно использовать тогда, когда число импликант, входящих в сокращенную форму функции невелико.
Отметим следующее свойство произвольной, в частности, сокращенной дизъюнктивной нормальной формы переключательной функции импликант:
- если из этой формы исключить одну или несколько импликант, то полученное после этого выражение будет обращаться в нуль на тех же наборах, что и исходное выражение.
Это связано с тем, что дизъюнктивная форма обращается в нуль только в том случае, когда все ее логические слагаемые равны нулю. Однако, при исключении импликанты может оказаться, что на тех наборах, на которых исключенная импликанта равнялась единице (а следовательно, вместе с ней и вся дизъюнкция равнялась единице ввиду соотношения 1Ú х 1=1), оставшееся выражение не будет равно единице. Если же проверкой установить, что при исключении импликанты полученное выражение равно единице на этих наборах, то можно утверждать, что все нули и все единицы обоих выражений совпадают и, следовательно, исключенная импликанта является лишней.
Таким образом, чтобы испытать некоторую импликанту, ее следует исключить из сокращенной дизъюнктивной нормальной формы и подставить в оставшееся выражение такие значения переменных, которые обращают исключенную импликанту в единицу. Если при этом оставшееся выражение будет тождественно равно единице, то испытываемая импликанта является лишней.
Применение этого правила связано с некоторыми особенностями, которые можно рассмотреть на примерах.
Пример 1. Найти тупиковые формы переключательной функции, заданной в сокращенной дизъюнктивной нормальной форме:
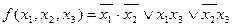 .
.
1. Испытываем импликанту 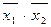 . Подставляем в
. Подставляем в 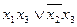 значения х 1 = 0 и х 2 = 0, т.к. при этом
значения х 1 = 0 и х 2 = 0, т.к. при этом 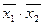 =
= 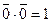 :
:
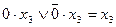
Следовательно, импликанту 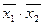 исключать нельзя, т.к. оставшееся выражение не равно тождественно единице.
исключать нельзя, т.к. оставшееся выражение не равно тождественно единице.
2. Импликанту х 1 х 3 исключать также нельзя, т.к. при х 1= 1 и х 3 = 1
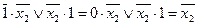
3. Для импликанты 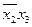 :
:
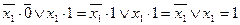
Полученное выражение тождественно равно единице, поэтому импликанту 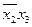 можно исключить, т.к. она является лишней.
можно исключить, т.к. она является лишней.
Пример 2. Упростить переключательную функцию.
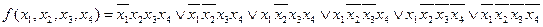 .
.
На основе теоремы Квайна получим
1¸2 ® 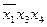
2¸3 ® 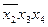
3¸4 ® 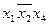
4¸5 ® 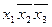
5¸6 ® 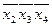
Тогда сокращенная ДНФ имеет вид
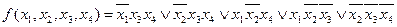 (2.4.1)
(2.4.1)
Найдем тупиковые формы.
1. Для 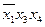 : х 1 = 0, х 3 = 1, х 4 = 1:
: х 1 = 0, х 3 = 1, х 4 = 1:
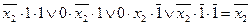
т.е. первую импликанту исключать нельзя.
2. Для 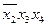 : х 2 = 0, х 3 = 1, х 4 = 1.
: х 2 = 0, х 3 = 1, х 4 = 1.
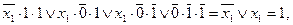
т.е. импликанта 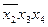 является лишней.
является лишней.
3. Проверяем третью импликанту 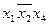 ; при этом вторую импликанту, которая оказалась лишней, вновь возвращаем в исследуемое выражение. Тогда, подставляя в выражение
; при этом вторую импликанту, которая оказалась лишней, вновь возвращаем в исследуемое выражение. Тогда, подставляя в выражение
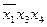 Ú
Ú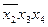 Ú
Ú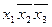 Ú
Ú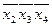
значения х 1 = 1, х 2 = 0, х 4 = 1, получим
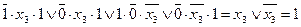 .
.
Следовательно, импликанта 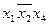 также лишняя и может быть исключена.
также лишняя и может быть исключена.
4. Аналогично можно показать, что и импликанту 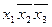 также может быть исключена.
также может быть исключена.
Таким образом выражение (2.4.1) имеет три лишние импликанты 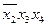
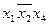 и
и 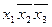 .
.
Однако исключать одновременно все лишние импликанты нельзя без дополнительной проверки. Вначале следует исключить одну импликанту полученного выражения. Исключим из выражения (24.1. импликанту 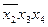 , получим
, получим
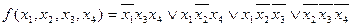
Вновь проверяем наличие лишних импликант, проверяя только те, которые были лишними при первой проверке, т.е. импликанты 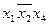 и
и 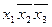 .
.
Подставляя в выражение
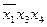 Ú
Ú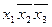 Ú
Ú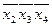
значения х 1 = 1, х 2 = 0, х 4 = 1 получаем
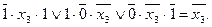
Следовательно, импликанту 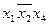 исключать нельзя, хотя при первой проверке, т.е. при наличии
исключать нельзя, хотя при первой проверке, т.е. при наличии 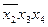 (тоже лишней), она была лишней.
(тоже лишней), она была лишней.
Поэтому если в некотором выражении имеется несколько лишних импликант, то исключение двух и более импликант одновременно без дополнительной проверки недопустимо.
2.5. Минимизация переключательных функций с помощью диаграмм Вейча
Диаграммы Вейча позволяют упростить поиск склеивающихся конституент. Диаграмма Вейча – это специальная таблица, определяющая значения переключательной функции на каждом наборе аргументов. Каждой клетке диаграммы соответствует определенный набор значений аргументов – рис. 2.5.1. б.
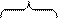 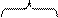 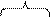    x 2 х 1 x 2 х 1 | x 2 x 2 x 2 x 2 x 2 x 2 | ||||||||||
   1 1 | х 1 х 1 | 1,1 | 1,0 | х 1 х 1 | х 1 x 2 | х 1 x 2 | х 1 х 1 | х 1Ú x 2 | х 1Ú x 2 | ||
| 0,1 | 0,0 | х 1 x 2 | х 1 x 2 | х 1Ú x 2 | х 1Ú x 2 |
(а) (б) (в) (г)
Рис. 2.5.1. Диаграмма Вейча для функции двух переменных.
Склеивающиеся между собой конституенты единицы или нуля в диаграммах Вейча для функций двух аргументов расположены в соседних клетках (рис. 2.5.1. в, г).
Чтобы представить переключательную функцию диаграммой Вейча следует записать единицы в клетки, соответствующие наборам, на которых функция равна единице, и нули – в остальные клетки.
В диаграмме Вейча для переключательной функции двух аргументов любая пара единиц, расположенных в соседних клетках, выражается одной буквой.
 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 | |||||||||||
| х 1 х 1 | х 1 х 1 | х 1 х 1 | х 1 х 1 | ||||||||

 f 2(х 1; x 2) = x 1 f 5(х 1; x 2) = x 2 f 12 = х 1 f 10 = х 2
f 2(х 1; x 2) = x 1 f 5(х 1; x 2) = x 2 f 12 = х 1 f 10 = х 2
Это обстоятельство используют для получения минимальных ДНФ и КНФ.
Рассмотрим диаграммы Вейча переключательной функции f 13(х 1; x 2) =
= х 1 ® x 2.
    x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 | Пара единиц во второй строке соответствует х 1, а пара единиц в | ||||||
   х 1 х 1 х 1 х 1 | х 1 х 1 | х 1 x 2 | первой колонке – x 2. f 13 (х 1; x 2 ) = х 1Ú x 2. | ||||
| х 1 x 2 | х 1 x 2 |
Это выражение, являющееся минимальной формой функции f 13 (x 1 ;x 2 ) получено путем склеивания конституент единиц, обведенных овалами.
|
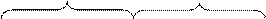 x 2 x 2 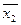 | ||||
 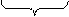 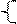  x 1 x 1 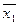 | x 1 x 2 x 3 | x 1 x 2 x 3 | x 1 x 2 x 3 | x 1 x 2 x 3 |
| x 1 x 2 x 3 | x 1 x 2 x 3 | x 1 x 2 x 3 | x 1 x 2 x 3 |
 x 3
x 3 
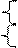   x 2 x 2  | ||||
   x 1 x 1 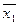 | x 1 Úx 2 Ú x 3 | x 1 Úx 2 Ú x 3 | x 1 Úx 2 Ú x 3 | x 1 Úx 2 Ú x 3 |
| x 1 Úx 2 Ú x 3 | x 1 Úx 2 Ú x 3 | x 1 Úx 2 Ú x 3 | x 1 Úx 2 Ú x 3 |
 x 3
x 3
x 2 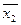 | ||||
x 1 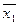 | ||||
 x 3
x 3
Рассмотрим диаграммы Вейча переключательных функций, которые выражаются произведением двух переменных
x 2 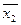 x 2 x 2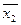 x 2 x 2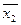 | ||||||||||||||
x 1 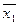 | x 1 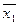 | x 1 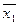 | ||||||||||||
 x 3
x 3
 x 3
x 3 
 x 3
x 3
x 1 x 2 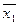 x 3
x 3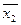 x 3
x 3
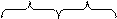      x 2 x 2 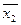 x 2 x 2 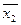 x 2 x 2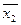 | ||||||||||||||
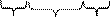 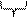 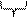 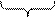 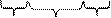 x 1 x 1 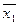 | x 1 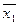 | x 1 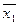 | ||||||||||||
 x 3
x 3 
 x 3
x 3
 x 3
x 3 
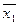
 x 1
x 1 x 1
x 1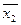
Четыре единицы, расположенные в соседних клетках, выражаются одной буквой.
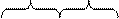 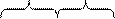 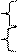    x 2 x 2 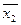 x 2 x 2 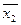 x 2 x 2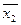 | ||||||||||||||
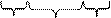 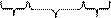 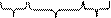 x 1 x 1 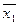 | x 1 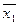 | x 1 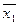 | ||||||||||||
 x 3
x 3
 x 3
x 3
 x 3
x 3 
x 3 

Чтобы построить диаграмму Вейча функции, заданной в СДНФ, нужно записать единицы в клетки диаграммы, которые соответствуют конституентам единицы данной функции.
Если функция задана в СКНФ, следует записать нули в клетки диаграммы, которые соответствуют конституентам нуля, входящим в данную функцию, а в остальных клетках записать единицы.
Отыскание минимальной ДНФ сводится к определению варианта, при котором все единицы диаграммы Вейча данной функции накрываются наименьшим числом наиболее коротких произведений.
 2014-02-13
2014-02-13 2516
2516








