В реальных кристаллах дислокации могут иметь только ограниченное число различных векторов Бюргерса. Для их определения удобно разбить все дислокации в кристаллах на следующие типы: 1. Полная дислокация; 2.Расщепленная или частичная.
Полной дислокацией является дислокация, которая не содержи никаких протяженных дефектов кроме своего узкого ядра и которая полностью окружена совершенным кристаллом. Дело в том, что энергия дислокации пропорциональна квадрату вектора Бюргерса, поэтому полные дислокации всегда должны иметь такие вектора Бюргерса, при которых они не могли бы понизить свою энергию путем разложения на 2 или большее число дислокаций.
 Обычно реализуется дислокация с 1 экстраплоскостью, т.е. так называемая единичная дислокация или дислокация единичной мощности. В принципе возможны дислокации, у которых вектор Бюргерса в целое число раз больше единичного, такие дислокации называются дислокациями n-кратной мощности. Ясно, что в этом случае искажение решетки около дислокации очень велико и по этой причине дислокации n-кратной мощности неустойчивые. И по этой причине они распадаются на n единичных дислокаций.
Обычно реализуется дислокация с 1 экстраплоскостью, т.е. так называемая единичная дислокация или дислокация единичной мощности. В принципе возможны дислокации, у которых вектор Бюргерса в целое число раз больше единичного, такие дислокации называются дислокациями n-кратной мощности. Ясно, что в этом случае искажение решетки около дислокации очень велико и по этой причине дислокации n-кратной мощности неустойчивые. И по этой причине они распадаются на n единичных дислокаций.
 В ГЦК, ОЦК и ГП решетках иногда существуют дислокационные вектора Бюргерса, которые не являются векторами тождественных трансляций, хотя в этом случае их энергия минимальна. Такие дислокации называются частичными.
В ГЦК, ОЦК и ГП решетках иногда существуют дислокационные вектора Бюргерса, которые не являются векторами тождественных трансляций, хотя в этом случае их энергия минимальна. Такие дислокации называются частичными.
Полная дислокация может расщепляться, диссоциировать на частичные и наоборот. Частичные дислокации могут объединяться в полную. Одни частичные дислокации могут рекомбинировать, давая другие частичные дислокации. Возможны другие варианты дислокационных реакций.
Сумма векторов Бюргерса исходных дислокаций должна быть равна сумме векторов Бюргерса – векторов дислокаций, получающихся в результате реакций 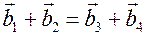 . Разнообразные дислокационные реакции подчиняются критерию Франка: реакция возможна в том случае, если сумма квадратов векторов Бюргерса исходных дислокаций больше суммы векторов Бюргерса дислокаций, являющихся результатами реакций. Этот критерий основан на:
. Разнообразные дислокационные реакции подчиняются критерию Франка: реакция возможна в том случае, если сумма квадратов векторов Бюргерса исходных дислокаций больше суммы векторов Бюргерса дислокаций, являющихся результатами реакций. Этот критерий основан на:
1. Энергия дислокации пропорциональна 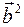
2. Реакция должна приводить к уменьшению энергии системы. Напрмер, дислокация может диссоциировать на 2: 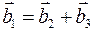 , если
, если 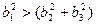 .
.
В противном случае диссоциация не возможна, если же 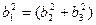 , то возникает неопределенность, т.е. критерий Франка не может предсказать реакцию. Однако возрастание энтропии указывает на возможность реакции.
, то возникает неопределенность, т.е. критерий Франка не может предсказать реакцию. Однако возрастание энтропии указывает на возможность реакции.
 2014-02-09
2014-02-09 4106
4106