Вектор Бюргерса используется в качестве меры оценки искажённости кристаллической решётки, обусловленной присутствием в ней дислокаций. Чтобы оценить степень искажённости решётки вызванной дислокацией, надо сравнить несовершенный кристалл с совершенным кристаллом. Для этого строят контур Бюргерса. Контур Бр. – замкнутый контур произвольной формы, построенный в реальном кристалле путем последовательного обхода дефекта от атома к атому в совершенной области кристалла.
 Нарисуем построение контура Бюргерса вокруг краевой дислокации. За исходную точку примем А. Пройдя вертикально вниз от атома к атому пять межатомных расстояний, отложим точку В. Аналогично, при прохождении пяти межатомных расстояний сначала вправо, затем от полученной точки С вверх, получим точку Д. Если от Д отложим пять межатомных расстояний, мы не попадем снова в точку А. Это будет новая точка Е. Чтобы замкнуть контур нужно соединить точки А и Е некоторым вектором
Нарисуем построение контура Бюргерса вокруг краевой дислокации. За исходную точку примем А. Пройдя вертикально вниз от атома к атому пять межатомных расстояний, отложим точку В. Аналогично, при прохождении пяти межатомных расстояний сначала вправо, затем от полученной точки С вверх, получим точку Д. Если от Д отложим пять межатомных расстояний, мы не попадем снова в точку А. Это будет новая точка Е. Чтобы замкнуть контур нужно соединить точки А и Е некоторым вектором
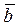 , называемым вектором Бюргерса. Разомкнутость контура обусловлена тем, что в кристалле имеется краевая дислокация, кромка экстраплоскости которой оказалась внутри контура Бюргерса. Поэтому путь обхода на верхнем участке контура оказался длиннее на одно межатомное расстояние. Вокруг дислокации атомы несколько смещены по сравнению с их расположением в идеальном кристалле. Сумма всех этих упругих смещений атомов, накопившихся при обходе контура Бюргерса, и проявляется в виде
, называемым вектором Бюргерса. Разомкнутость контура обусловлена тем, что в кристалле имеется краевая дислокация, кромка экстраплоскости которой оказалась внутри контура Бюргерса. Поэтому путь обхода на верхнем участке контура оказался длиннее на одно межатомное расстояние. Вокруг дислокации атомы несколько смещены по сравнению с их расположением в идеальном кристалле. Сумма всех этих упругих смещений атомов, накопившихся при обходе контура Бюргерса, и проявляется в виде 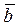 . Т.о.
. Т.о. 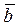 - мера искажения решетки, вызванная дислокацией. Величина
- мера искажения решетки, вызванная дислокацией. Величина
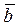 не зависит от того, насколько контур Бюргерса удален от дислокации. Случай винтовой дислокации можно построить следующим образом.
не зависит от того, насколько контур Бюргерса удален от дислокации. Случай винтовой дислокации можно построить следующим образом.
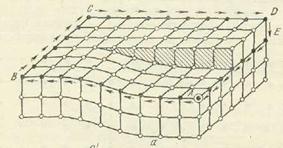 От точки А пройдем влево 7 межатомных расстояний до точки В, 6 межатомных расстояний до С вверх и вправо 7 до Д. Но для того, чтобы вернуться в А, в точке Е нужно совершить скачок на одно межатомное расстояние вниз. Т.о. и в этом случае вектором, ликвидирующим разомкнутость контура Бюргерса, является вектор Бюргерса. Направление последнего зависит от направления обхода по контуру Бюргерса. Следовательно, в понятии вектора Бюргерса содержится неопределенность, но этот недостаток не является существенным. Вектор Бюргерса (
От точки А пройдем влево 7 межатомных расстояний до точки В, 6 межатомных расстояний до С вверх и вправо 7 до Д. Но для того, чтобы вернуться в А, в точке Е нужно совершить скачок на одно межатомное расстояние вниз. Т.о. и в этом случае вектором, ликвидирующим разомкнутость контура Бюргерса, является вектор Бюргерса. Направление последнего зависит от направления обхода по контуру Бюргерса. Следовательно, в понятии вектора Бюргерса содержится неопределенность, но этот недостаток не является существенным. Вектор Бюргерса (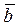 ) характеризуется рядом особенностей:
) характеризуется рядом особенностей:
1) 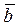 нормален к линии краевой дислокации и параллелен линии винтовой дислокации. Вдоль линии смешанной дислокации угол между последней и
нормален к линии краевой дислокации и параллелен линии винтовой дислокации. Вдоль линии смешанной дислокации угол между последней и 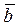 в разных точках имеет разную величину;
в разных точках имеет разную величину;
2) 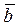 у дефектов не дислокационного типа равен нулю, т. е. если построить контур Бюргерса вокруг любой точки дефекта, цепочки вакансий или межузельных атомов, то соответствующий контур окажется замкнутым;
у дефектов не дислокационного типа равен нулю, т. е. если построить контур Бюргерса вокруг любой точки дефекта, цепочки вакансий или межузельных атомов, то соответствующий контур окажется замкнутым;
3) 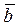 одинаков вдоль всей линии дислокации, т. е. является инвариантом дислокации. Это следует из того, что при смещении контура Бюргерса вдоль линии дислокации, он все время будет оставаться эквивалентным исходному контуру.
одинаков вдоль всей линии дислокации, т. е. является инвариантом дислокации. Это следует из того, что при смещении контура Бюргерса вдоль линии дислокации, он все время будет оставаться эквивалентным исходному контуру.
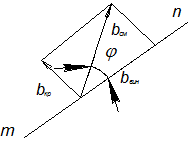
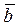 смешанной дислокации можно разложить на краевую и винтовую компоненты, которые зависят от угла
смешанной дислокации можно разложить на краевую и винтовую компоненты, которые зависят от угла 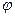 между
между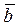 и линией смешанной дислокации.
и линией смешанной дислокации.
Из инвариантности 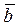 вытекает важное следствие: дислокации не могут обрываться внутри кристалла.
вытекает важное следствие: дислокации не могут обрываться внутри кристалла. 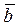 и линии дислокации однозначно определяют возможную плоскость скольжения. Величину
и линии дислокации однозначно определяют возможную плоскость скольжения. Величину 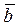 или его мощность определяют по формуле:
или его мощность определяют по формуле:
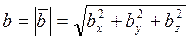 ,
,
где 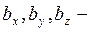 составляющие
составляющие 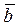 по координатным осям. За направления координатных осей обычно принимают кристаллографические направления ребер элементарной ячейки данной решетки.
по координатным осям. За направления координатных осей обычно принимают кристаллографические направления ребер элементарной ячейки данной решетки.
Если 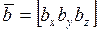 , то в случае кубической решетки
, то в случае кубической решетки 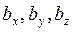 можно выразить через период элементарной ячейки, а
можно выразить через период элементарной ячейки, а 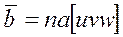 , где u, v, w – символы кристаллографического направления
, где u, v, w – символы кристаллографического направления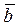 в примитивной кубической решетке. Компоненты
в примитивной кубической решетке. Компоненты 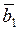 по координатным осям:
по координатным осям: 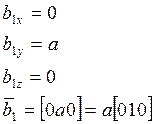
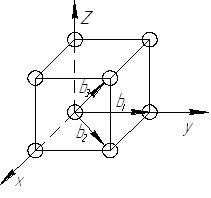 Это значит, что направление
Это значит, что направление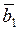 является кристаллограничным направлением
является кристаллограничным направлением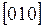 , а его мощность будет равна
, а его мощность будет равна 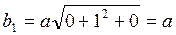
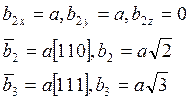
 2014-02-09
2014-02-09 4394
4394








