Если матрица А системы линейных уравнений невырожденная, т.е.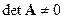 , то матрица А имеет обратную, и решение системы (5.3) совпадает с вектором C = A -1 B. Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X = C, C = A -1 B называют матричным способом решения системы, или решением по методу обратной матрицы.
, то матрица А имеет обратную, и решение системы (5.3) совпадает с вектором C = A -1 B. Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X = C, C = A -1 B называют матричным способом решения системы, или решением по методу обратной матрицы.
Пример 2.15. Решить матричным способом систему уравнений
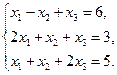
Решение. Обозначим
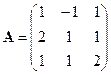 ;
;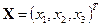
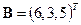
Тогда данная система уравнений запишется матричным уравнением AX = B. Поскольку 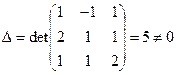 , то матрица A невырождена и поэтому имеет обратную:
, то матрица A невырождена и поэтому имеет обратную:
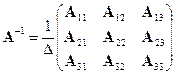 .
.
Для получения решения X мы должны умножить вектор-столбец B слева на матрицу A: X = A -1 B. В данном случае
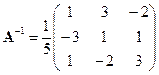
и, следовательно,
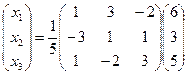 .
.
Выполняя действия над матрицами, получим:
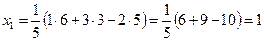 ,
,
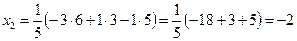 ,
,
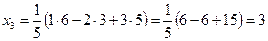 .
.
Итак, 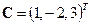 .
.
 2014-02-09
2014-02-09 527
527







