Условие. Содержание отчета к заданию

Содержание отчета к заданию.

Задание для выполнения контрольной работы.

Варианты заданий изложены в таблице 3.

1. Построить алгоритм решения обыкновенное дифференциальное уравнение первого порядка на отрезке [a, b], шаг h = 0.1 и h = 0.01, для каждого метода, указанного в табл.3 и составить соответствующий алгоритм вычисления в среде табличного процессора Excel.

2. Все вычисления вести с четырьмя десятичными знаками после запятой.

3. Сравнить результаты вычисления различных методов с различными шагами интегрирования.

Таблица 3 – варианты обыкновенных дифференциальных уравнений для решения численными методами.

№ п/п	Уравнения	Методы
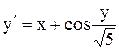	[1.8;2.8] y(1.8)=2.6	Эйлера и Рунге-Кутта II порядка
	y¢=x+cos(y/3) [1.6;2.6] y(1.6)=4.6	Эйлера и Рунге-Кутта II порядка
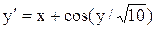	[0.6;1.6] y(0.6)=0.8	Эйлера и Рунге-Кутта II порядка
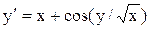	[0.5;1.5] y(0.5)=0.6	Эйлера и Рунге-Кутта II порядка
	y¢=x+cos(y/p) [1.7;2.7] y(1.7)=5.3	Эйлера и Рунге-Кутта II порядка
	y¢=x+cos(y/2.25) [1.4;2.4] y(1.4)=4.2	Эйлера и Рунге-Кутта II порядка
	y¢=x+cos(y/e) [1.4;2.4] y(1.4)=2.5	Эйлера и Рунге-Кутта II порядка
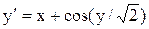	[0.8;1.8] y(0.8)=1.4	Эйлера и Рунге-Кутта II порядка
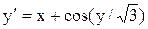	[1.2;2.2] y(1.2)=2.1	Эйлера и Рунге-Кутта II порядка
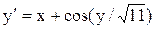	[2.1;3.1] y(2.I)=2.5	Эйлера и Рунге-Кутта II порядка
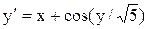	[1.8;2.8] y(1.8)=2.6	Эйлера и Рунге-Кутта II порядка
	y¢=x+sin(y/3) [1.6;2.6] y(1.6)=4.6	Эйлера и Рунге-Кутта II порядка
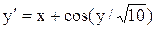	[0.6;1.6] y(0.6)=0.8	Эйлера и Рунге-Кутта II порядка
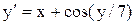	[0.5;1.5] y(0.5)=0.6	Эйлера и Рунге-Кутта II порядка
	y¢=x+sin(y/p) [1.7;2.7] y(1.7)=5.3	Эйлера и Рунге-Кутта II порядка
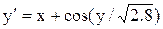	[1.4;2.4] y(1.4)=2.2	Модифицированный Эйлера и Рунге-Кутта IV порядка
	y¢=x+sin(y/e) [1.4;2.4] y(1.4)=2.5	Модифицированный Эйлера и Рунге-Кутта IV порядка
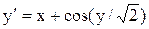	[0.8;1.8] y(0.8)=1.3	Модифицированный Эйлера и Рунге-Кутта IV порядка
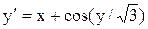	[1.1;2.1] y(1.I)=1.5	Модифицированный Эйлера и Рунге-Кутта IV порядка
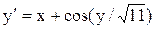	[0.6;1.6] y(0.6)=1.2	Модифицированный Эйлера и Рунге-Кутта IV порядка
	y¢=x+sin(y/1.25) [0.5;1.5] y(0.5)=1.8	Модифицированный Эйлера и Рунге-Кутта IV порядка
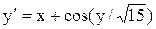	[0.2;1.2] y(0.2)=1.1	Модифицированный Эйлера и Рунге-Кутта IV порядка
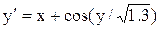	[0.1;1.1] y(0.I)=0.8	Модифицированный Эйлера и Рунге-Кутта IV порядка
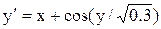	[0.5;1.5] y(0.5)=0.6	Модифицированный Эйлера и Рунге-Кутта IV порядка
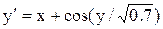	[1.2;2.2] y(1.2)=1.4	Модифицированный Эйлера и Рунге-Кутта IV порядка
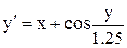	[0.4;1.4] y(0.4)=0.8	Модифицированный Эйлера и Рунге-Кутта IV порядка
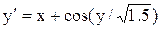	[0.3;1.3] y(0.3)=0.9	Модифицированный Эйлера и Рунге-Кутта IV порядка
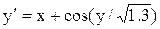	[1.2;2.2] y(1.2)=1.8	Модифицированный Эйлера и Рунге-Кутта IV порядка
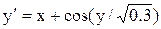	[0.7;1.7] y(0.7)=2.1	Модифицированный Эйлера и Рунге-Кутта IV порядка
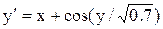	[0.9;1.9] y(0.9)=1.7	Модифицированный Эйлера и Рунге-Кутта IV порядка

В отчете необходимо предъявить:

• алгоритм решения задания в среде табличного процессора Excel, реализующий вычислительную схему каждого из методов;
• файл, содержащий реализацию использованных методов в среде табличного процессора Excel;

· анализ результатов и выводы.

Пример выполнения задания.

Используя модифицированный метод Эйлера и метод Рунге-Кутта IV порядка построить численное решение дифференциального уравнения: 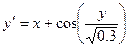при заданных начальных условиях: y(0.7)= 2.1 на отрезке [0.7;1.7].

Расчеты провести в среде табличного про­цессора Excel с шагом h=0.1 и h=0.01. Все вычисления вести с четырьмя десятичными знаками после запятой.

Сравнить результаты вычисления различных методов с различными шагами интегрирования.