Правило резолюции (или резолюция) уже рассматривалось во второй главе. Это правило гласит, что из истинности двух дизъюнкций, одна из которых содержит дизъюнкт, а другая — его отрицание, следует (выводима) формула, являющаяся дизъюнкцией исходных формул без упомянутого дизъюнкта и его отрицания. Резолюция записывалась в следующем виде:
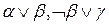 ├
├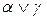 или эквивалентно
или эквивалентно 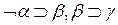 ├
├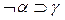 .
.
В логике предикатов первого порядка она выглядит так же. Формулы 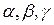 в ней являются формулами этой логики. Введем по аналогии с обобщенным правилом модус поненс обобщенное правило резолюции, или обобщенную резолюцию:
в ней являются формулами этой логики. Введем по аналогии с обобщенным правилом модус поненс обобщенное правило резолюции, или обобщенную резолюцию:
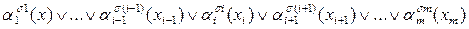 ,
,
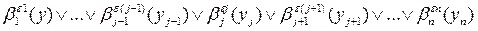 ,
,
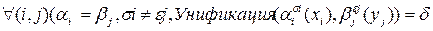 ├
├
Подстановка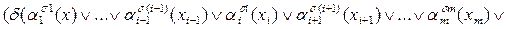
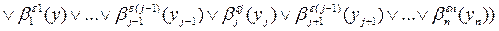 .
.
Здесь  , i = 1,..., п обозначает литерал, такой, что
, i = 1,..., п обозначает литерал, такой, что  =
= 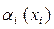 , при
, при 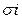 = 1 и
= 1 и  =
=  при
при 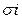 = 0. Аналогичный смысл имеет символ
= 0. Аналогичный смысл имеет символ 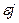 в литерале
в литерале 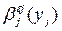 , j = 1,..., m. Подстановка
, j = 1,..., m. Подстановка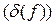 означает формулу, получающуюся из формулы f в результате подстановки
означает формулу, получающуюся из формулы f в результате подстановки 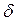 во все ее атомы. Суть обобщенного правила модус поненс можно выразить следующим образом. Если существует истинная формула
во все ее атомы. Суть обобщенного правила модус поненс можно выразить следующим образом. Если существует истинная формула
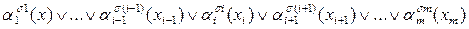
являющаяся дизъюнкцией литералов  , i = 1,..., п, и истинная формула
, i = 1,..., п, и истинная формула
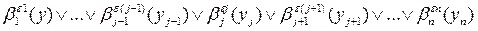
также являющаяся дизъюнкцией литералов 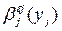 , j = 1,..., m, и в этих формулах предикатные символы литералов
, j = 1,..., m, и в этих формулах предикатные символы литералов  и
и 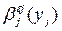 одинаковы (
одинаковы (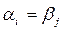 ),
), 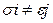 , и для атомов
, и для атомов  и
и 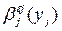 существует унификация
существует унификация 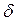 , делающая их одинаковыми (записывается как Унификация
, делающая их одинаковыми (записывается как Унификация 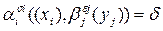 ), то можно вывести истинную формулу, получающуюся в результате подстановки
), то можно вывести истинную формулу, получающуюся в результате подстановки 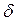 в дизъюнкцию исходных формул после удаления в них литералов
в дизъюнкцию исходных формул после удаления в них литералов  и
и 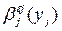 . Выведенную таким образом истинную формулу называют резольвентой. Так же как и в случае резолюции для логики высказываний, обобщенную резолюцию можно выразить с использованием импликации. Обратим внимание, что исходные формулы в обобщенной резолюции и резольвента являются дизъюнкцией литералов. Обычно такие формулы называют клаузальными формами, или клаузами. Таким образом, использование резолюции для вывода требует клаузальной формы представления знаний. Это, в свою очередь, означает, что база знаний, вывод для которой осуществляется на основе обобщенной резолюции, должна представлять собой совокупность клауз, понимаемых в целом как формула, являющаяся конъюнкцией клауз. Формулы такого типа обычно называют конъюнктивными нормальными формулами.
. Выведенную таким образом истинную формулу называют резольвентой. Так же как и в случае резолюции для логики высказываний, обобщенную резолюцию можно выразить с использованием импликации. Обратим внимание, что исходные формулы в обобщенной резолюции и резольвента являются дизъюнкцией литералов. Обычно такие формулы называют клаузальными формами, или клаузами. Таким образом, использование резолюции для вывода требует клаузальной формы представления знаний. Это, в свою очередь, означает, что база знаний, вывод для которой осуществляется на основе обобщенной резолюции, должна представлять собой совокупность клауз, понимаемых в целом как формула, являющаяся конъюнкцией клауз. Формулы такого типа обычно называют конъюнктивными нормальными формулами.
 2014-02-09
2014-02-09 666
666








