Преобразование произвольной формулы логики предикатов первого порядка в клаузальную форму

Применение обобщенного правила резолюции требует представления формул в клаузальной форме. В этом разделе покажем, с помощью каких эквивалентных преобразований любая произвольная формула логики предикатов первого порядка может быть преобразована в клаузальную форму. Процедуру преобразования представим в виде отдельных шагов.

Исключение импликаций. Из логики высказываний известно, что 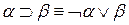. Поэтому на первом шаге с помощью этой формулы исключаем все импликации.

Перемещения знака отрицания ( ) непосредственно к атомам. В клаузах отрицание допустимо только перед атомами. Поэтому используя перечисленные ниже законы Де Моргана, эквивалентности кванторов и двойного отрицания, перемещаем знак отрицания непосредственно к атомам:

,

,

,

,

.

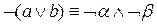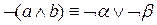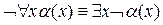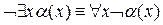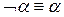Переименование переменных. Во всех формулах, в которых встречаются кванторы, использующие одни и те же связанные переменные, как, например, в формуле 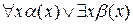, переименовываем связанные переменные таким образом, чтобы они были индивидуальными для каждого квантора. Например, для нашего примера это может быть использование переменной у вместо переменной д: для квантора существования. В результате получится формула .

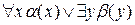Перемещение кванторов влево. После предыдущего шага, в результате которого каждый квантор использует свои связанные переменные, обозначения которых не совпадают с переменными других кванторов, все кванторы перемещаем влево. Так, например, простая формула 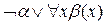после перемещения квантора влево примет вид .

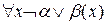Сколемизация. Сколемизацией называется специфический прием удаления кванторов существования. В простейшем случае — это замена формулы 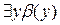на формулу 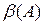, где А является константой, ранее не встречавшейся. В общем случае, когда переменная, связываемая квантором существования, встречается в каком-либо литерале вместе с переменными, связанными квантором общности, приходится, чтобы избавиться от квантора общности, вводить специальную функцию, зависящую от переменных, связанных квантором общности, вместо переменной, связанной квантором существования.

Так, если имеем формулу

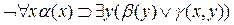
то здесь литерал 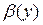может означать, например, наличие некоторого свойства, именуемого предикатным символом 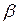, у объекта, именуемого переменной у, а атом 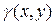задает отношение между объектами х, у. Объект, обозначенный переменной у, определяется в этом случае значением переменной х и может быть заменен на ранее не встречавшуюся функцию F(x), называемую обычно функцией Сколема. После такой замены квантор существования может быть удален, а формула приобретает вид

.

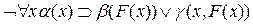Распределение конъюнкций относительно дизъюнкций. Это распределение осуществляется на основе использования дистрибутивного закона

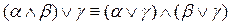
Перемещение скобок к концу и началу. На этом шаге формулы со скобками типа 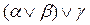или 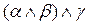приводятся соответственно к виду 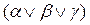или 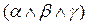. После этого шага исходная формула преобразуется в нормальную конъюнктивную форму, являющуюся конъюнкцией дизъюнкций литералов. Каждая дизъюнкция литералов является клаузой.