Вернемся теперь к примеру с кубиками и повторим прямой вывод той же целевой формулы, но уже используя обобщенную резолюцию. Заметим, что формулы (4.130), (4.135) уже являются клаузами. Остальные формулы с помощью простейших преобразований на основе закона 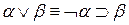 легко преобразуются в клаузы. В результате вместо (4.136) — (4.141) получим следующие формулы.
легко преобразуются в клаузы. В результате вместо (4.136) — (4.141) получим следующие формулы.
Формулы, определяющие условия выполнения действий:
 на (х, у)
на (х, у)  свободен (х)
свободен (х)  переместить (х, Стол), (4.151)
переместить (х, Стол), (4.151)
 на (х, Стол)
на (х, Стол)  свободен (х)
свободен (х)  свободен (z)
свободен (z) 
 переместить (х, z). (4.152)
переместить (х, z). (4.152)
Формулы, определяющие условия переходов состояний среды:
 на (х, у)
на (х, у)  свободен (х)
свободен (х)  переместить (х, Стол)
переместить (х, Стол) 
 на (х, Стол), (4.153)
на (х, Стол), (4.153)
 на (х, у)
на (х, у)  свободен (х)
свободен (х)  переместить (х, Стол)
переместить (х, Стол) свободен (у), (4.154)
свободен (у), (4.154)  на (х, у)
на (х, у)  свободен (х)
свободен (х)  свободен (z)
свободен (z) 
 переместить (х, z)
переместить (х, z)  на (х, z), (4.155)
на (х, z), (4.155)
 на (х, у)
на (х, у)  свободен (х)
свободен (х)  свободен (z)
свободен (z) 
 переместить (х, z)
переместить (х, z)  свободен (у). (4.156)
свободен (у). (4.156)
Целевая формула. Целевая формула в соответствии с рис. 4.1 является конъюнкцией литералов и при прямом выводе, как и в случае использования обобщенного правила модус поненс, будет выводиться для каждого литерала, входящего в ее состав, раздельно
на (А, В) 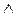 на (В, Стол)
на (В, Стол) 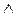 на (С, Стол)
на (С, Стол) 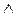 на (D, Стол). (4.157)
на (D, Стол). (4.157)
Вывод. Используя унифицированные клаузы (4.130), (4.151), которые после унификации превращаются в клаузы (4.158), (4.159), получаем резольвенту (4.160):
на (A, C), (4.158)
 на (А, С)
на (А, С)  свободен (A)
свободен (A)  переместить (А, Стол), (4.159)
переместить (А, Стол), (4.159)
 свободен (A)
свободен (A)  переместить (А, Стол). (4.160)
переместить (А, Стол). (4.160)
Используя клаузы (4.134)(свободен (А), (4.134)), (4.160), получаем резольвенту
переместить (А, Стол). (4.161)
Используя эту резольвенту и унифицированную клаузу (4.154), которая после унификации превратилась в клаузу (4.162), получаем резольвенту (4.163):
 на (А, у)
на (А, у)  свободен (A)
свободен (A)  переместить (А, Стол)
переместить (А, Стол) 
 свободен (у), (4.162)
свободен (у), (4.162)
 на (А, у)
на (А, у)  свободен (A)
свободен (A)  свободен (у). (4.163)
свободен (у). (4.163)
Затем, используя клаузы (4.130), (4.134) и унифицированный резольвент (4.163), получаем резольвенту
свободен (С). (4.164)
Аналогично можем получить следующие резольвенты:
на (А, Стол), (4.165)
переместить (D, Стол), (4.166)
свободен (В), (4.167)
на (D, Стол). (4.168)
Итак, кубики А и D могут быть перемещены на стол, в результате чего кубики В и С окажутся свободными. После этого, используя клаузы (4.134), (4.135), (4.165) и клаузу (4.152), которая после унификации превращается в клаузу (4.169), получаем резольвенту (4.170)
 на (А, Стол)
на (А, Стол)  свободен (A)
свободен (A)  свободен (В)
свободен (В) 
 переместить (А, В), (4.169)
переместить (А, В), (4.169)
переместить (А, В). (4.170)
Наконец, воспользовавшись клаузами (4.134), (4.135), (4.165), (4.170) и клаузой (4.155), которая после унификации превращается в клаузу (4.171), получим резольвенту (4.172):
 на (А, Стол)
на (А, Стол)  свободен (A)
свободен (A)  свободен (В)
свободен (В) 
 переместить (А, В)
переместить (А, В)  на (А, В), (4.171)
на (А, В), (4.171)
на (А, В). (4.172)
Таким образом, снова имеем истинные атомы на (А, В), на (В, Стол), на (С, Стол), на (D, Стол). Согласно правилу введения конъюнкции, вновь делаем заключение об истинности целевой формулы на (А, В) 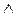 на (В, Стол)
на (В, Стол) 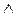 на (С, Стол)
на (С, Стол) 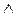 на (D, Стол). На этом прямой вывод с использованием обобщенного правила резолюции завершен.
на (D, Стол). На этом прямой вывод с использованием обобщенного правила резолюции завершен.
Достоинством использования обобщенного правила резолюции для прямого вывода является способность выводить большее количество формул по сравнению с выводом на основе обобщенного правила модус поненс. В процессе вывода база знаний по-прежнему разрастается за счет занесения в нее вновь выводимых формул. Некоторые из этих формул могут оказаться ненужными для вывода целевой формулы.
Как уже говорилось, Робинсон предложил использовать обобщенную резолюцию для создания стратегии вывода, в основе которой лежит опровержение или доведение до противоречия. Идея этой стратегии вывода состоит в следующем. Предположим необходимо вывести истинность целевой формулы  . Делается опровержение этой формулы, т.е. предполагается истинным ее отрицание
. Делается опровержение этой формулы, т.е. предполагается истинным ее отрицание 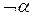 . Эта формула, являющаяся отрицанием целевой, заносится в базу знаний. После этого, если, начиная обратный вывод с формулы
. Эта формула, являющаяся отрицанием целевой, заносится в базу знаний. После этого, если, начиная обратный вывод с формулы 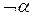 , удастся установить противоречие, т.е. вывести пару литералов
, удастся установить противоречие, т.е. вывести пару литералов 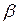 и
и 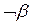 , то считается, что сделанное предположение об истинности отрицания целевой формулы ошибочно (опровергнуто) и делается заключение об истинности целевой формулы
, то считается, что сделанное предположение об истинности отрицания целевой формулы ошибочно (опровергнуто) и делается заключение об истинности целевой формулы  . Если в результате рассмотрения всех возможных путей вывода такого противоречия установить не удастся, то считается, что целевая формула является ложной.
. Если в результате рассмотрения всех возможных путей вывода такого противоречия установить не удастся, то считается, что целевая формула является ложной.
Рассмотрим стратегию обратного вывода на основе опровержения для примера с кубиками.
 2014-02-09
2014-02-09 686
686








