2014-02-09
1190
Лекция 13 – Метод динамического программирования
2. Основное функциональное уравнение Беллмана.
3. Примеры.
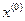- начальное состояние динамической системы S.
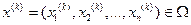- состояние системы на k-том шаге, где k=1,2,…,N.
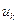- управление, обеспечивающее переход системы из состояния 
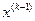в состояние 
, 
.
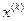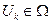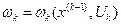- определённый выигрыш, который обеспечен в результате реализации k-того шага.
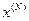- конечное состояние системы S.
P – общий выигрыш за N шагов.
N – конечное число шагов.
Задача ДП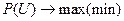 
.
<…>
Требуется найти такое уравнение U, в результате реализации которого система S переходит из начального состояния в конечное, при чём функция P(U) достигает своего экстремального значения, при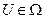 
.
Пусть ЗДП удовлетворяет двум условиям:
1) Отсутствие последействия
Новое состояние системы 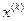зависит только от данного состояния системы 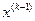и выбранного управления 
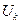и не зависит от того, каким образом система пришла в состояние .
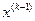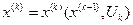
2) Аддитивность и.ф.
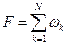(1)
Общий выигрыш за N шагов равен сумме выигрышей за каждый из N шагов.
В основе метода ДП лежит идея постепенной, пошаговой оптимизации. Однако планируя многошаговую оптимизацию надо выбрать на каждом шаге управление таким образом, чтобы учитывать его последствия на следующих шагах.
Условно оптимальное уравнение – каждое уравнение 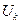, выбранное при определённых предположениях о том, как окончился предыдущий шаг, и обеспечивающее экстремальное значение функции выигрыша 
.
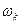Оптимальное управление (оптимальная стратегия управления) – совокупность управлений
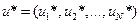
, в результате которой система S за N шагов переходит из начального состояния 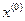в конечное 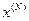, и при этом функция (1) принимает экстремальное значение.
Принцип оптимальности:
Оптимальная стратегия такова, что каковы бы ни были начальное состояние и начальные решения, последующие решения должны приниматься исходя из оптимальной стратегии с учётом состояний, получающихся в результате первого решения.
Из принципа оптимальности следует 1-я специфическая особенность метода ДП: процесс решения задачи разворачивается от конца к началу; прежде всего планируется последний шаг решения задачи.
Идея многошаговой процедуры:
· Управление на k-том шаге планируют так, чтобы была максимальна (минимальна) сумма выигрышей на всех оставшихся до конца шагах, плюс данныйШТО?.
· Последний, N-ный шаг, планируют так, чтобы он сам принёс наибольший (наименьший) выигрыш.
Процесс ДП:
· Планируется последний, N-ный шаг, исходя из предположений о том, чем закончился предпоследний, (N-1)-ый шаг. Для каждого такого предположения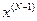 
находят условно оптимальное управление 
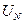и соответствующий ему условный оптимальный выигрыш 
.
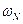· Планируется предпоследний, (N-1)-ый шаг, исходя из предположений о том, чем закончился предпоследний, (N-2)-ой шаг. Для каждого такого предположения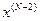 
находят условно оптимальное управление 
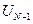, при котором выигрыш за последние 2 шага максимален.
· Далее оптимизируют управление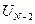 
, по не доходят до 1-го шага и управления 
.
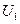· Оптимальная стратегия управления будет состоять из оптимальных шаговых управлений:
.
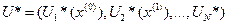Отметим 2-ю специфическую особенность метода ДП: многошаговый процесс проходят дважды. Первый раз – от конца к началу, в результате чего находят условно оптимальное управление и условно оптимальные выигрыши. Второй раз – от начала к концу, в результате чего находят оптимальное управление u*, состоящее из оптимальных шаговых управлений.
Замечание. Принцип погружения.
Природа задачи ДП не зависит от количества шагов N, то есть форма ЗДП инвариантна относительно N.
Реализация принципов оптимальности и погружения гарантирует то, что решение на очередном шаге является наилучшим относительно всего процесса ДП.
