Рис.7.9
Рис.7.6
Классификация аналого-цифровых преобразователей
По принципу действия:
- время- импульсного преобразования,
- частото - импульсного преобразования,
- развертывающего преобразования.
АЦП развертывающего преобразования имеют следующие разновидности;
· поразрядно уравновешивания,
· с линейно изменяющимся компенсационным напряжением,
· со ступенчато изменяющимся компенсационным напряжением.
АЦП время – импульсного преобразования.
Время – импульсный метод преобразования основан на преобразовании измеряемой величины х в интервал времени tx, который заполняется импульсами образцовой частоты с периодом T0.
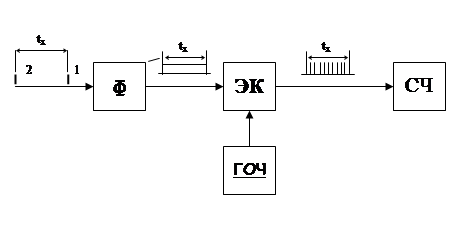 |
Рис. 7.5.
Блок – схема АЦП время – импульсного преобразования представлена на рис.7.5. Из схемы следует, что измеряемый интервал времени tx задается короткими импульсами 1 («пуск») и 2 («стоп»), которые воздействуя на формирователь Ф (триггер), создают на его выходе импульс прямоугольной формы длительностью tx.
Этот импульс открывает электронный ключ ЭК и на счетчик СЧ начинают поступать импульсы с ГОЧ с периодом T0. За время tx на счетчик поступит N импульсов.
Таким образом, измеряемый интервал времени tx равен
tx = T0 N
Источником погрешности АЦП время- импульсного преобразования могут быть:
- нестабильность частоты ГОЧ, что приводит к изменению периода T0,
- погрешность дискретности, обусловленной тем, что за число периодов T0, определяющих интервал времени tx, принимается число импульсов N, поступивших на счетчик,
- отсутствие синхронизации между измеряемым импульсом 1 исследуемым интервалом времени tx и частотой сигналов ГОЧ.
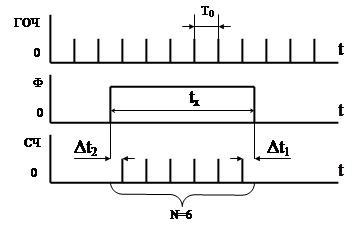 |
На рис.7.6 показано заполнение измеряемого интервала времени tx, представленного длительностью импульса прямоугольной формы, импульсами ГОЧ с периодом T0.
Из рисунка следует, что за время tx, на счетчик поступит число импульсов N=6. Следовательно, интервал времени tx = NT0 = 6T0.
Действительное значение tx = 6T0 + Dt1 + Dt2
где Dt1 – погрешность, обусловленная отсутствием синхронизации между импульсом управления 1 и частотой ГОЧ,
Dt2 - погрешность дискретизации.
Таким образом, максимальная погрешность измерения интервала времени tx составит
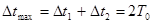 ,
,
а относительная погрешность
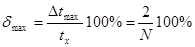 ,
,
где T0 – шаг дискретизации
Для устранения погрешности 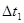 необходимо импульс 1 формировать на основе ГОЧ, а погрешность
необходимо импульс 1 формировать на основе ГОЧ, а погрешность 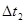 - путем использования схема с «электронным нониусом».
- путем использования схема с «электронным нониусом».
Измерение частоты электрических сигналов
Измерение частоты электрических сигналов с использованием электронно-счетных частотомеров может быть выполнено методом прямой и обратной функции.
Метод прямой функции (МПФ) основан на считывание числа периодов исследуемого сигнала, частоту которого необходимо определить. При этом между частотой исследуемого сигнала fx и числом импульсов (периода) N за образцовый интервал времени To устанавливается прямая связь
fx=F(N).


Рис. 7.7
На рис. 7.7 представлены временные диаграммы преобразования исследуемого сигнала по методу прямой функции. Из временной диаграммы следует, что
To=NTx=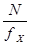 .
.
Тогда можно написать
fx=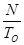 ,
,
где Т – число импульсов, поступивших на счетчик, To – образцовый интервал времени, который может принимать следующие значения …0,01; 0,1; 1; 10; 1000с…. Цифры получены из общего выражения To=10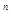 , где n=0;
, где n=0; 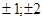 …
…
При To=1 получим
fx=N, Гц.

На рис. 7.8 представлена блок-схема частотомера, работающего по методу прямой функции, в которой образцовый интервал времени To формирует датчик интервала времени (ДИВ).
При синхронизации напряжения Ux с образцовым интервалом времени (как это показано на рис. 7.7) погрешность измерения частоты fx определяется потерей одного импульса. Таким образом абсолютная погрешность измерения частоты составит

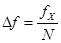 ,
,
а относительная погрешность
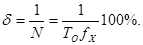


На рис. 7.9 представлено семейство характеристик 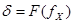 для нескольких значений To (0,1; 1; 10; 100с).
для нескольких значений To (0,1; 1; 10; 100с).
Из графиков следует:
- относительная погрешность измерения частоты уменьшается с увеличением частоты,
- относительная погрешность увеличивается с уменьшением интервала времени To.
Метод обратной функции (МОФ) основан на измерение периода Tx исследуемого сигнала путем заполнения его импульсами образцовой частоты fо. если за время Tx укладывается N импульсов образцовой частоты, то устанавливается следующая функциональная связь
fx=F(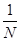 ).
).


Рис. 7.10
На рис. 7.10 представлены временные диаграммы преобразования исследуемого сигнала по методу обратной функции. Из временной диаграммы следует, что за время одного периода Tx измеряемого напряжения Ux укладывается N периодов To образцового напряжения, и можно написать так Tx=NTo. Следовательно частота
fx=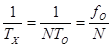 .
.

Рис.7.11
На рис. 7.11 представлена блок-схема частотомера, в который в образцовый интервал времени To формирует ГОУ (генератор образцовой частоты).
При синхронизации сигнала напряжения Ux и ГОУ абсолютная погрешность измерения частоты составит
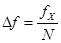 ,
,
а относительная погрешность
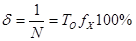 .
.


Рис.7.12
На рис. 7.12 представлено семейство характеристик 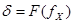 для нескольких значений fo (10
для нескольких значений fo (10 ; 10
; 10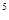 ; 10
; 10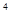 и 10
и 10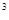 Гц).
Гц).
Из графиков следует:
- относительная погрешность измерения частоты уменьшается с уменьшением частоты fx,
- относительная погрешность увеличивается с увеличением частоты.
Из анализа графиков рис. 7.9 и 7.12 следует, что МПФ измерения целесообразно использовать на средних и высоких частотах сигналов, так как он дает меньшие погрешности измерения. На низких частотах меньшие погрешности измерения дает МОФ.
Следовательно, при широком диапазоне измеряемых частот сигналов необходимо разделить его на два поддиапазона разделительной частотой fразд, определяемой допустимым значением относительной погрешности 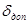 .
.
Приравнивая относительные погрешности измерения прямого 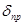 и обратного
и обратного 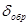 методов (
методов (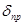 =
=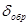 =
=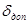 ) получим
) получим
fразд=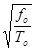 .
.
Например, при 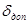 =0.1%, To=1с и fo=10
=0.1%, To=1с и fo=10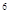 Гц получим fразд=10
Гц получим fразд=10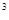 Гц.
Гц.
На рис. 7.13 представлен график для рассмотренного примера.

Рис.7.13
Понятие фазовый сдвиг относит к двум гармоническим сигналам (напряжение, ток) одной и той же частоты.
В случае негармонических сигналов понятие фазовый сдвиг заменяется понятием сдвиг во времени.


Рис.7.14
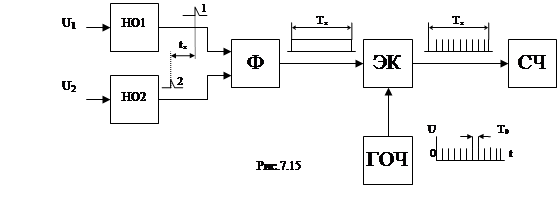

На рис.7.4 представлены временные диаграммы преобразования фазового сдвига 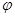 в цифровой код с промежуточным преобразованием во временной интервал, а на рис.7.15 блок-схема фазометра.
в цифровой код с промежуточным преобразованием во временной интервал, а на рис.7.15 блок-схема фазометра.
Из схемы следует, что изменяемый интервал времени tx пропорциональный фазовому сдвигу 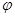 , формируется импульсами управления (ИУ) 1 и 2, которые поступают с выхода ноль-органов НО1 и НО2 (компараторов) в момент перехода напряжений U1 иU2 через ноль. Дальнейшее преобразование интервала времени tx в код описан в разделе АЦП время-импульсного преобразования.
, формируется импульсами управления (ИУ) 1 и 2, которые поступают с выхода ноль-органов НО1 и НО2 (компараторов) в момент перехода напряжений U1 иU2 через ноль. Дальнейшее преобразование интервала времени tx в код описан в разделе АЦП время-импульсного преобразования.
Можно написать следующее соотношение
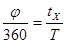
Из которого следует выражение для измеряемого фазового сдвига
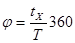
Учитывая, что tx=ToN, получим
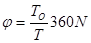
 2014-02-09
2014-02-09 579
579







