Модели миграции

Пример

Интенсивность заражения	0.2
Интенсивность выздоровления	0.02
Начальное число больных	0.005

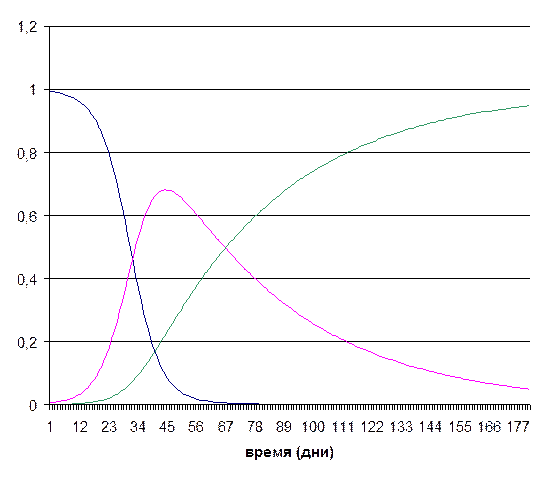
не болевшие больные выздоровевшие

Численное решение дифференциальных уравнений и систем. Проще всего воспользоваться методом Эйлера. Уравнение с одной неизвестной функцией

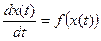
заменяется конечно-разностным уравнением

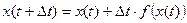
Аналогично, система дифференциальных уравнений

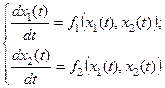
заменяется системой конечно-разностных уравнений

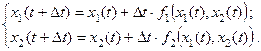
Применительно к рассматриваемой модели эпидемии система конечно-разностных уравнений имеет вид

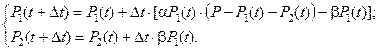
при начальном условии P ₁(0) = 0; P ₂(0) = 0.

1. Рассмотрим вначале два множества (кластера), численности которых x ₁ и x ₂. Введем характеристики подвижности a₁ и a₂: подвижность a₁ есть отношение величины потока (числа перемещающихся в единицу времени) покидающих множество 1 и направляющихся в множество 2; подвижность a₂ определяется аналогично. Динамика численностей описывается дифференциальным уравнением

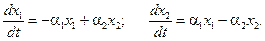
Ясно, что x ₁+ x ₂= N = const. Равновесные численности (dx ₁ /dt = 0, dx ₂ /dt = 0):

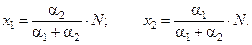
2. Пусть число кластеров равно m, их численности x_i, i =1, …, m, подвижности теперь имеют направления: a _ij, i, j =1, …, m, i ¹ j.

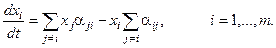
Положим

a _ii = 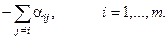(1)

определим матрицу A = (a _ij) _m _´ _m и вектор-строку x = (x_i)₁_´ _m. В этих обозначениях

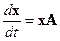Равновесные численности должны отвечать системе xA = 0; но матрица A — вырожденная (A1 = 0), и если вектор x > 0 — равновесный, то и вектор k x — также равновесный при любом k >0. Поэтому система xA = 0 определяет лишь равновесные пропорции, а для равновесных численностей следует задать еще и общую численность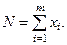

3. Помимо m множеств рассматривается еще и внешняя среда. Она предполагается «большой» в том смысле, что число объектов в ней велико (≈ ∞), подвижность в направлении рассматриваемых множеств ничтожна (≈ 0), так что к i -му кластеру направлен поток с конечной интенсивностью l _i, а от i -го кластера во внешнюю среду направлен поток, определяемый подвижностью a _i _, _m _{+ 1}; ни тот, ни другой поток не изменяют численности объектов во внешней среде.

С учетом обозначения (1) теперь динамика численностей описывается системой уравнений

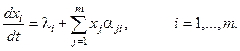
При этом суммы в (1) должны содержать слагаемые a _i _, _m _{+ 1}. Ввод в рассмотрение вектора-строки l = (l _i)₁_´ _m позволяет описать динамику равенством

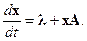
Равновесные численности теперь описываются системой l + xA = 0.

Пример. Пусть m = 3, a₁₂ = 0.1, a₁₃ = 0.2, a₂₃= 0.4, a₂₄= 0.3, a₃₁ = 0.5; таким образом,

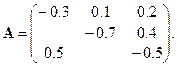
Входные потоки: l₁ = 400, l₃ = 200, так что l = (400, 0, 200). (Не указанные числовые значения равны нулю.) Равновесные значения численностей определяются условием

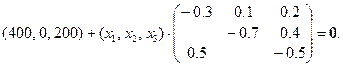
Решением этой системы уравнений служат равновесные численности

x ₁ = 1400; x ₂ = 2000; x ₃ = 7600.

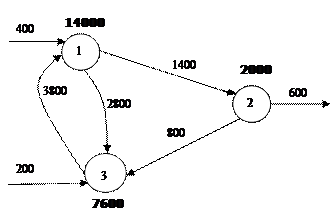Решение представлено на рисунке. Над кластерами жирным шрифтом показаны равновесные численности, над дугами показаны равновесные интенсивности потоков.