Статистическое изучение связи. (4 ч)
Исследуя природу, общество, экономику, необходимо считаться с взаимосвязью наблюдаемых процессов и явлений. При этом полнота описания, так или иначе, определяется количественными характеристиками причинно-следственных связей между ними. Оценка наиболее существенных из них, а также воздействия одних факторов на другие является одной из основных задач статистики.
Общие формы проявления связи между явлениями:
1) функциональная (полная) – жестко детерминированная;
2) корреляционная (неполная) – статистическая или стохастически детерминированная.
Функциональная связь - если с изменением значения одной из переменных вторая изменяется строго определенным образом, то есть значению одной переменной обязательно соответствует одно или несколько точно заданных значений другой переменной. Функциональная связь двух величин возможна лишь при условии, что вторая из них зависит только от первой и ни от чего более.
Статистическая связь - если с изменением значения одной из переменных вторая может в определенных пределах принимать любые значения с некоторыми вероятностями, но ее среднее значение или другие статистические (массовые) характеристики изменяются по определенному закону. То есть при статистической связи разным значениям одной переменной соответствуют разные распределения значений другой переменной.
Корреляционная связь - важнейший частный случай статистической связи, состоящей в том, что разным значениям одной переменной соответствуют различные средние значения другой.
Корреляционная связь проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятных значений независимой переменной. Т.е. некоторое увеличение аргумента влечет за собой лишь среднее увеличение или уменьшение функции, тогда как конкретные значения у отдельных единиц наблюдения будут отличаться от среднего.
По направлению связи бывают:
1. прямые - когда зависимая переменная растет с увеличением факторного признака;
2. обратные - при которых рост аргумента сопровождается уменьшением функции. Такие связи также называют соответственно положительными и отрицательными.
Относительно своей аналитической формы связи бывают линейными и нелинейными. В первом случае, между признаками в среднем проявляются линейные соотношения. Нелинейная взаимосвязь выражается нелинейной функцией, а переменные связаны между собой в среднем не линейно.
С точки зрения взаимодействующих факторов связи подразделяют:
1. парные - если характеризуется связь двух признаков;
2. множественные - если изучаются более чем две переменные.
Различают непосредственные, косвенные и ложные связи. В первом случае факторы взаимодействуют между собой непосредственно. Для косвенной связи характерно участие какой-то третьей переменной, которая опосредует связь между изучаемыми признаками. Ложная связь – связь, установленная формально и, как правило, подтвержденная только количественными оценками. Она не имеет под собой качественной основы или же бессмысленна.
По силе различаются слабые и сильные связи. Эта формальная характеристика выражается конкретными величинами и интерпретируется в соответствии с общепринятыми критериями силы связи для конкретных показателей. При этом вычисление коэффициента корреляции заключается не только в выявлении связи между явлениями, но и в количественной характеристике этой связи. Коэффициент корреляции ( ) находится в пределах от -1 до +1
) находится в пределах от -1 до +1
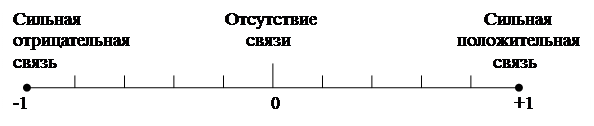 |
Рисунок 9
Методы оценки тесноты связи подразделяются на корреляционные ( параметрические ) и непараметрические.
Рассмотрим на примерах положительную, отрицательную взаимосвязь, и отсутствие таковой.
Положительная взаимосвязь присутствует в функции производства, когда с ростом цен на производимую продукцию, возрастает желание производителей выпускать большее количество товаров (рис. 2а). Так же к положительной взаимосвязи можно отнести следующие явления в жизни:
- чем выше доходы, тем большие требования предъявляются к качеству жизни;
- чем больше клиентов, тем выше прибыль (в обычных рыночных условиях);
- чем выше посещаемость студентами занятий, тем выше их успеваемость и т.д.
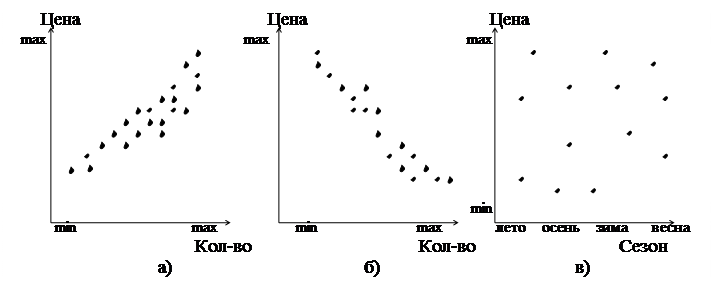
Рисунок 10 –Виды взаимосвязи
Отрицательная взаимосвязь проявляется в функции потребительского спроса. Чем ниже цены, тем больше желающих покупать товар. А с ростом цен спрос на товары снижается (рис 10 б). Приведем следующие примеры отрицательной связи:
- чем «старше» автомобиль тем ниже на него цена (исключение – раритетные авто);
- чем выше температура на улице, тем меньше требуется одежды;
- увеличение дополнительной занятости студента (работа, семья) снижает успеваемость (чаще всего, хотя бывают и исключения).
Об отсутствии взаимосвязи говорят, когда один признак никаким образом на другой не влияет. Например, цена на хлеб не зависит от сезона (рис 10 в). Рост, размер одежды, цвет глаз и волос на успеваемость студента не влияет. Цвет автомобиля может повлиять на его цену, а вот на скоростные характеристики влияния не оказывает. В современном мире идет борьба за то, чтобы пол и возраст человека на его должность и з/плату не влиял.
В корреляционном анализе важно разделять все признаки на факторные (х) и результативные (у). Факторные признаки оказывают влияние. Результативные - испытывают влияние. Один и тот же признак в различных условиях может быть факторным и результативным (рис 11). Рассмотрим пример.
1 вариант. Прибыль магазина зависит от цен на товары, вежливости обслуживания, ассортимента и пр. В этом случае Прибыль - результативный признак, испытывающая влияние перечисленных факторных признаков. Высокая цена - низкая прибыль, удачное место расположения - высокая прибыль и т.д.
2 вариант. После получения, прибыль можно направить на расширение магазина, на выплату премий работникам, положить в банк и т.д. В этом случае уже прибыль становится факторным признаком и влияет на результативные (премии, расширение и пр.). Большая прибыль – расширение торговых площадей, низкая прибыль – отсутствие премии и т.д.
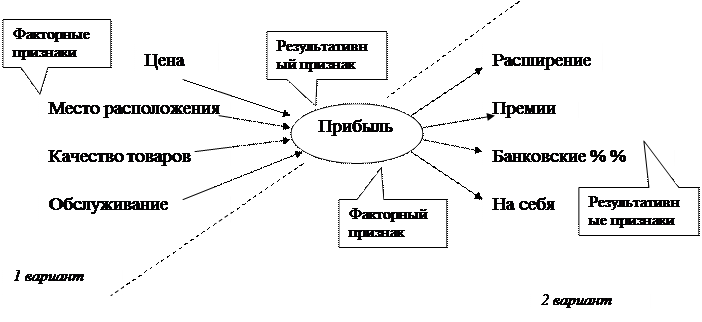
Рисунок 11– Факторные и результативные признаки
Условия применения корреляционно-регрессионного анализа:
1. наличие данных по достаточно большой совокупности. По отдельным явлениям можно получить искаженное представление о связи признаков или обнаружить ложную связь;
2. надежное выражение закономерности в средней величине. Для этого необходима достаточная однородность совокупности;
3. необходимость подчинения распределения совокупности по результативному и факторным признакам нормальному закону распределения вероятностей. На практике это условие чаще всего выполняется приближенно, но и тогда корреляционно-регрессионный анализ дает хорошие результаты.
Этапы корреляционного анализа:
1) Логический анализ сущности изучаемого явления и взаимосвязей. На этой стадии устанавливают объект наблюдения, выявляют различные показатели. Среди них определяют факторные и результативные признаки. На этой же стадии следует понять истинная или ложная корреляционная связь в изучаемом явлении. Ложную корреляционную связь можно продемонстрировать на известном примере с пожарными командами.
Таблица 7
| Размер населенного пункта | Количество пожарных команд | Количество пожаров (в год) |
| малый | ||
| средний | ||
| большой |
На первый взгляд присутствует прямая корреляционная зависимость между этими показателями. То есть чем больше пожарных команд, тем больше пожаров случается. На самом деле это не так, чем больше город – тем больше в нем жителей. Чем больше жителей, тем чаще возникают пожароопасные ситуации. И как следствие большее количество пожарных требуется для обеспечения безопасности.
2) Сбор информации и ее первичная обработка (метод группировки, графический метод), проверка достаточной однородности совокупности. Проверка подчинения распределения совокупности по результативному и факторным признакам нормальному закону распределения вероятностей.
Для проверки однородности совокупности используют показатели вариации:
Среднее квадратическое отклонение:
по не сгруппированным данным - 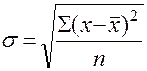 ;
;
по сгруппированным данным - 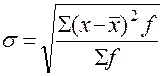 ,
,
где (f –частота повторения признака).
Коэффициент вариации - 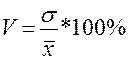 . Совокупность считается однородной при V <33%.
. Совокупность считается однородной при V <33%.
Проверка подчинения распределения совокупности нормальному закону распределения проводится по правилу «3 σ» (трех сигм). Для этого полученное распределение по совокупности сравнивают с нормой (табл.2):
Таблица 8.
| № | Интервалы | Ко-во единиц входящих в интервал | Удельный вес единиц, по отношению к общей численности, % | Норма распределения, % |
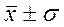 | 68,3 | |||
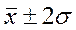 | 95,4 | |||
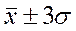 | 99,7 |
Пример. Рассмотрим взаимосвязь между ценой квартир и количеством комнат.
Таблица
| № квартиры | Кол-во комнат (х) | Цена, тыс. руб. (у) | 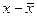 | 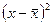 |
| 1 | 2 | 3 | 4 | 5 |
| 1-2,2 = -1,2 | -1,22=1,44 | |||
| 2-2,2 = -0,2 | -0,22= 0,04 | |||
| 1-2,2 = -1,2 | -1,22= 1,44 | |||
| 4-2,2 = 1,8 | 1,82= 3,24 | |||
| 2-2,2 = -0,2 | -0,22= 0,04 | |||
| 3-2,2 = 0,8 | 0,82= 0,64 | |||
| 1-2,2 = -1,2 | -1,22= 1,44 | |||
| 1-2,2 = -1,2 | -1,22= 1,44 | |||
| 2-2,2 = -0,2 | -0,22= 0,04 | |||
| 5-2,2 = 2,8 | 2,82= 7,84 | |||
| итого | 17,6 |
Факторный признак – количество комнат (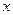 ). Именно это (а так же район, состояние, этаж и пр.) влияет на стоимость квартиры – результативный признак (
). Именно это (а так же район, состояние, этаж и пр.) влияет на стоимость квартиры – результативный признак (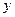 ).
).
Найдем среднее значение по факторному признаку:
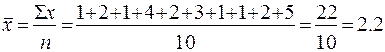 (примерно 2 комнаты для всей совокупности).
(примерно 2 комнаты для всей совокупности).
Рассчитаем среднее квадратическое отклонение. Для этого проведем дополнительные расчеты в 4 и 5 столбце:
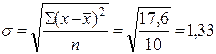 .
.
Найдем коэффициент вариации:
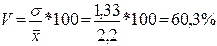 (
(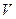 >33%).
>33%).
Совокупность не однородная. Полученные усредненные данные могут существенно отличаться от индивидуальных значений.
Проанализируем распределение совокупности на соответствие нормальному закону распределения с помощью правила «3 σ»
Найдем интервалы:
1 интервал. 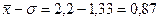 - нижняя граница интервала,
- нижняя граница интервала,
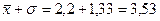 - верхняя граница интервала);
- верхняя граница интервала);
2 интервал. 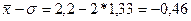 - нижняя граница интервала,
- нижняя граница интервала,
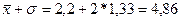 - верхняя граница интервала;
- верхняя граница интервала;
3 интервал. 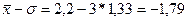 - нижняя граница интервала,
- нижняя граница интервала,
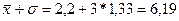 - верхняя граница интервала.
- верхняя граница интервала.
На рисунке интервалы представлены в наглядной форме.
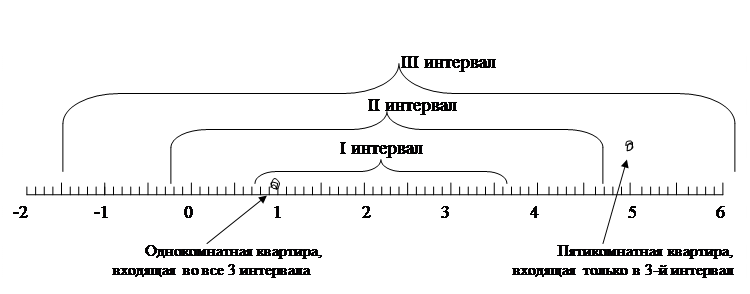
Рисунок: Границы 3-х интервалов
Нижние границы 2-го и 3-го интервалов получились с отрицательным знаком (фактически “- 0,46” комнаты и “–1,79” комнаты). Теоретически такого быть не может. Однако в виду неоднородности совокупности и сильного разброса индивидуальных единиц от средней, такие интервалы возникают. Интервалы с минусом показывают широкий диапазон вариантов входящих в него.
При распределении некоторые из квартир будут входить во все 3 интервала, некоторые только во 2-й и 3-й. А некоторые только в 3-й.
Таблица
| № | Интервалы | Кол-во единиц (квартир) | Удельный вес единиц,, % | Норма распределения, % |
| 1 | 2 | 3 | 4 | 5 |
| 0,87-3,53 | 8 квартир | (8/10)*100 =80% | 68,3 | |
| -0,46-4,86 | 9 квартир | (9/10)*100 =90% | 95,4 | |
| -1,79-6,19 | 10 квартир | (10/10)*100 =100% | 99,7 |
В первый интервал войдут квартиры с номерами:
№1 (1 комната), №2 (2 комнаты), №3 (1 комната), №5 (2 комнаты), №6 (3 комнаты), №7 (1 комната), №8 (1 комната), №9 (2 комнаты) – итого 8 квартир.
Во второй интервал войдут все квартиры кроме десятой (пятикомнатной). В третий интервал попадут все 10 квартир.
Сравнивая полученное распределение (столбец 4) с нормой распределения (столбец 6) видим, что 2 и 3-й интервалы не сильно отличаются от нормы. А вот 1-й интервал имеет существенное отклонение от нормы распределения.
Получив распределение, проанализируем данные на существенность отклонения от нормы. Если отклонения существенны, стоит принят решение об отказе от дальнейших исследований (с этими данными), так как полученные результаты будут неадекватно оценивать рассматриваемое явление.
Если в исследуемой совокупности немного единиц с резко выделяющимися данными (резко отклоняющимися от среднего значения) следует эти единицы удалить из анализируемых данных. Так, если бы в рассмотрении участвовала семикомнатная квартира (такое бывает, но очень редко) её следовало бы удалить их всей совокупности квартир, и проводить расчеты с оставшимися единицами (квартирами). Основным критерием, по которому принимают решение об удалении единиц из совокупности, является непопадание единиц в третий интервал (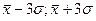 ).
).
3) Установление зависимости и определение ее направления. Для этого применяют метод аналитической группировки и рассчитывают групповые средние. Так же рассчитывают первые разности или строят поле корреляции (график по факторному и результативному признаку). Пример. Рассмотрим эти методы на примере взаимосвязи между ежемесячным среднедушевым доходом и затратами на питание (в тыс. руб.).
Таблица
| № человека | ||||||||||
| затраты на питание | 3,1 | 1,1 | 6,5 | 7,0 | 3,4 | 2,8 | 3,0 | 3,4 | 5,5 | 4,0 |
| з/плата | 5,0 | 2,0 | 12,0 | 18,0 | 6,0 | 4,0 | 5,0 | 5,0 | 9,0 | 7,0 |
| № человека | ||||||||||
| затраты на питание | 2,5 | 3,5 | 2,0 | 1,5 | 5,0 | 4,7 | 3,9 | 4,0 | 5,0 | 2,9 |
| з/плата | 3,5 | 6,0 | 2,5 | 2,3 | 10,0 | 11,0 | 7,0 | 7,5 | 8,5 | 4,0 |
Затраты на питание – это результативный признак, на который влияет факторный признак – з/плата.
3.1) Построение аналитической группировки. Построим группировку по факторному признаку (з/плата) с равными интервалами и числом групп - 4. Для этого ширину интервала (шаг) рассчитаем по формуле:
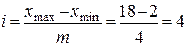 .
.
Зависимость расходов на питание от зарплаты представим в виде табл.:
Таблица
| интервал | Варианты зарплат и затрат на питание | сумма | кол-во человек | средняя | |||||||||||
| от 2 до 6 | з/плата | 2,0 | 5,0 | 6,0 | 4,0 | 5,0 | 5,0 | 3,5 | 6,0 | 2,5 | 2,3 | 4,0 | 45,3 | 11,0 | 4,1 |
| расходы на питание | 1,1 | 3,1 | 3,5 | 2,8 | 3,0 | 3,4 | 2,5 | 3,4 | 2,0 | 1,5 | 2,9 | 29,2 | 2,7 | ||
| от 6 до 10 | з/плата | 9,0 | 7,0 | 10,0 | 7,0 | 7,5 | 8,5 | 49,0 | 8,2 | ||||||
| расходы на питание | 5,5 | 4,0 | 5,0 | 3,9 | 4,0 | 5,0 | 27,4 | 4,6 | |||||||
| от 10 до 14 | з/плата | 12,0 | 11,0 | 23,0 | 11,5 | ||||||||||
| расходы на притание | 6,5 | 4,7 | 11,2 | 5,6 | |||||||||||
| от 14 до 18 | з/плата | 18,0 | 18,0 | 18,0 | |||||||||||
| расходы на питание | 7,0 | 7,0 | 7,0 |
В последнем столбце таблицы рассчитали среднюю зарплату и средние расходы на питание по группе. С увеличением зарплаты, растут затраты на питание. Можно предположить наличие положительной корреляционной связи.
3.2) Расчетный метод нахождения первых разностей по результативному признаку. Для этого составим ранжированный вариационный ряд по факторному признаку. Продолжим пример: Первым, в этом ряду стоит человек с порядковым № 2 – у него самая низкая з/плата, замыкает ряд человек с номером 4 - он обладатель самой высокой зарплаты. Затем в этом ряду вычислим первые разности (на сколько каждый из вариантов расходов на питание отличается от предыдущего). Например человек с номером 14 находится в ряду на 2 месте по з/плате (2,3 тыс.руб.). Вычитаем из показателя его расходов на питание (1,5 тыс.руб.) значение расходов человека, с стоящего перед ним в ряду (человек №2 с расходами на питание 2 тыс.руб.). Разница между этими расходами составляет 0,4 тыс.руб. (1,5 -1,1) и т.д.
Таблица
| № | з/плата (х) | затраты на питание (у) | первые разности результативного признака у' |
| 2,0 | 1,1 | ||
| 2,3 | 1,5 | 0,4 | |
| 2,5 | 2,0 | 0,5 | |
| 3,5 | 2,5 | 0,5 | |
| 4,0 | 2,8 | 0,3 | |
| 4,0 | 2,9 | 0,1 | |
| 5,0 | 3,1 | 0,2 | |
| 5,0 | 3,0 | -0,1 | |
| 5,0 | 3,4 | 0,4 | |
| 6,0 | 3,4 | 0,0 | |
| 6,0 | 3,5 | 0,1 | |
| 7,0 | 4,0 | 0,5 | |
| 7,0 | 3,9 | -0,1 | |
| 7,5 | 4,0 | 0,1 | |
| 8,5 | 5,0 | 1,0 | |
| 9,0 | 5,5 | 0,5 | |
| 10,0 | 5,0 | -0,5 | |
| 11,0 | 4,7 | -0,3 | |
| 12,0 | 6,5 | 1,8 | |
| 18,0 | 7,0 | 0,5 |
В последней колонке видим различие в затратах на питание между соседними вариантами, ранжированными по уровню з/платы. Различие колеблется от -0,5 до 1,8 тыс. руб. В среднем различие составляет 300-400 руб. и темпы его роста примерно одинаковы. Следовательно, можно предположить что связь существует.
3.3) Построение поля корреляции по факторному и результативному признаку (рис.11). Если исходные данные (значения переменных х и у) нанести на график в виде точек в прямоугольной системе координат, то получим поле корреляции. При этом значения независимой переменной х (признак-фактор) откладываются по оси абсцисс, а значения результирующего фактора у откладываются по оси ординат. Если зависимость у от х функциональная, то все точки расположены на какой-то линии. При корреляционной связи вследствие влияния прочих факторов точки не лежат на одной линии, но все же их расположение обнаруживает определенную тенденцию.
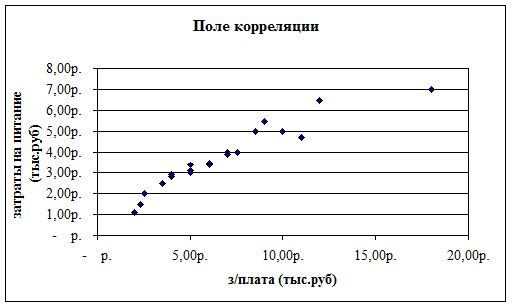
Рисунок 11 – Графическое изображение зависимости между факторным и результативным признаком при исследовании взаимосвязи между з/платой и расходами на питание.
Анализ графика показывает, что все точки выстраиваются в некоторую воображаемую прямую линию (с некоторыми отклонениями). Такой вид распределения вариантов на плоскости свидетельствует о тесной взаимосвязи между рассматриваемыми признаками.
Для проверки гипотез о форме связи используют также другой графический метод – построение эмпирической линии регрессии. Эмпирическая линия регрессии (эмпирическая регрессия) - ломаная линия, изображающая изменение групповых средних результативного признака в зависимости от изменения группировочного признака-фактора. Форма эмпирической регрессии дает возможность проверить, соответствует ли фактическое соотношение признаков тому или иному теоретически предполагаемому их соотношению. Для построения эмпирической линии регрессии используем данные аналитической группировки, представленные в таблице 7.
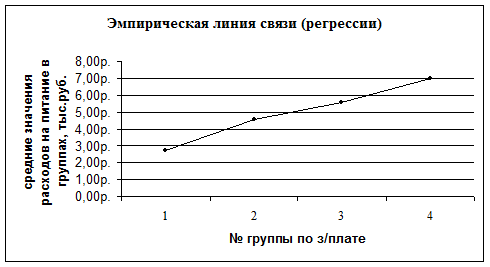
Рис. 7. Зависимость расходов на питание от з/платы.
4) Оценка существенности взаимосвязи между признаками с помощью показателей силы и тесноты связи:
Коэффициент корреляции - (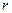 )
)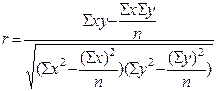 , где n – количество исследуемых единиц (в нашем примере – количество людей). Коэффициент корреляции принимает значения в интервале от –1 до +1. Если величина коэффициента отрицательная, то связь обратная, если положительная – связь прямая. Считают, что если этот коэффициент не больше 0,30, то связь слабая; от 0,3 до 0,7 – средняя; больше 0,7 – сильная, или тесная. Когда коэффициент равен 1, то связь функциональная, если он равен 0, то говорят об отсутствии линейной связи между признаками.
, где n – количество исследуемых единиц (в нашем примере – количество людей). Коэффициент корреляции принимает значения в интервале от –1 до +1. Если величина коэффициента отрицательная, то связь обратная, если положительная – связь прямая. Считают, что если этот коэффициент не больше 0,30, то связь слабая; от 0,3 до 0,7 – средняя; больше 0,7 – сильная, или тесная. Когда коэффициент равен 1, то связь функциональная, если он равен 0, то говорят об отсутствии линейной связи между признаками.
Пример. Рассчитаем коэффициент корреляции по данным из таблицы 5. к предыдущему примеру. Все необходимые расчеты занесем в таблицу:
Таблица
| № | з/плата (х) | затраты на притание (у) | 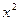 |  | 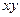 |
| 5,0 | 3,1 | 9,61 | 15,5 | ||
| 2,0 | 1,1 | 1,21 | 2,2 | ||
| 12,0 | 6,5 | 42,25 | |||
| 18,0 | 7,0 | ||||
| 6,0 | 3,4 | 11,56 | 20,4 | ||
| 4,0 | 2,8 | 7,84 | 11,2 | ||
| 5,0 | 3,0 | ||||
| 5,0 | 3,4 | 11,56 | |||
| 9,0 | 5,5 | 30,25 | 49,5 | ||
| 7,0 | 4,0 | ||||
| 3,5 | 2,5 | 12,25 | 6,25 | 8,75 | |
| 6,0 | 3,5 | 12,25 | |||
| 2,5 | 2,0 | 6,25 | |||
| 2,3 | 1,5 | 5,29 | 2,25 | 3,45 | |
| 10,0 | 5,0 | ||||
| 11,0 | 4,7 | 22,09 | 51,7 | ||
| 7,0 | 3,9 | 15,21 | 27,3 | ||
| 7,5 | 4,0 | 56,25 | |||
| 8,5 | 5,0 | 72,25 | 42,5 | ||
| 4,0 | 2,9 | 8,41 | 11,6 | ||
| Сумма | 135,3 | 74,8 | 1203,29 | 324,74 | 614,1 |
Рассчитаем коэффициент корреляции:
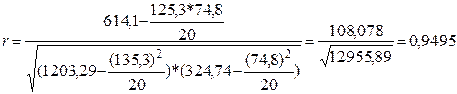 .
.
Полученный коэффициент близок к единице, что свидетельствует о прямой, положительной и очень тесной взаимосвязи между уровнем зарплаты и расходами на питание, которые увеличиваются с ростом объемов заработка.
Коэффициент детерминации – это отношение межгрупповой дисперсии результативного признака, к общей дисперсии результативного признака, выражающей влияние на него всех причин и условий:
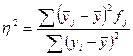 ,
,
где 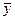 - общее среднее значение;
- общее среднее значение;
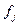 - частота в
- частота в 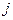 -й группе;
-й группе;
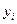 - значение результативного признака для
- значение результативного признака для 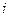 -й единицы;
-й единицы;
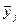 - среднее значение
- среднее значение 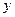 в
в 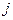 -й группе.
-й группе.
Межгрупповая дисперсия (факторная дисперсия) результативного признака выражает влияние различий группировочного факторного признака на среднюю величину результативного признака. Факторная дисперсия характеризует вариацию результативного признака, объясняемую только признаком-фактором. Остаточная дисперсия объясняется влиянием прочих факторов на результативный признак. Общая дисперсия складывается за счет влияния всех факторов. Коэффициент (индекс) детерминации – отношение факторной дисперсии к общей, показывает какая часть общей вариации результативного признака, объясняется признаком-фактором.
Непараметрические показатели связи. Непараметрические методы разработаны для переменных, измеренных на номинальной или порядковой шкале.Непараметрические методы не накладывают ограничений на закон распределения изучаемых величин. Их преимуществом является простота вычислений. Непараметрические методы наиболее приемлемы, когда объем данных невелик (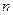 <100).
<100).
Измерение на номинальной шкале – указание градации признака 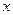 для данного объекта.
для данного объекта.
Порядковая шкала устанавливает некоторый порядок следования объектов.
Измерение связи между неколичественными переменными основано на таблице сопряженности – двух- или трехмерном распределении единиц совокупности. Если изучается связь между признаками, каждый из которых принимает два значения (дихотомические переменные), то данные представляются в таблице сопряженности 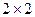 и вычисляются специальные меры связи: коэффициенты ассоциации, коэффициенты контингенции:
и вычисляются специальные меры связи: коэффициенты ассоциации, коэффициенты контингенции:
Коэффициент ассоциации (Юла) -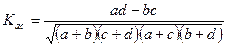 принимает значения в интервале
принимает значения в интервале 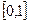 : 0 – отсутствие связи, 1 – полная связь. Коэффициент ассоциации принимает значение «1», если хотя бы одна из клеток таблицы
: 0 – отсутствие связи, 1 – полная связь. Коэффициент ассоциации принимает значение «1», если хотя бы одна из клеток таблицы 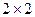 равна нулю. Поэтому важно учитывать эту особенность при интерпретации результатов измерения связи.
равна нулю. Поэтому важно учитывать эту особенность при интерпретации результатов измерения связи.
Коэффициент контингенции (Пирсона) - 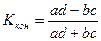 является более достоверной мерой связи между дихотомическими переменными, принимает значения в интервале
является более достоверной мерой связи между дихотомическими переменными, принимает значения в интервале 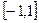 : 0 – отсутствие связи, 1 или -1 – полная связь. Коэффициент контингенции имеет недостаток: при равных нулю одного из двух гетерогенных сочетаний
: 0 – отсутствие связи, 1 или -1 – полная связь. Коэффициент контингенции имеет недостаток: при равных нулю одного из двух гетерогенных сочетаний 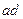 или
или 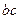 коэффициент обращается в единицу.
коэффициент обращается в единицу.
Коэффициент ассоциации дает более осторожную оценку тесноты связи, коэффициент контингенции – завышает ее.
Для расчета этих коэффициентов строится таблица сопряженности 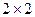 для записи основных данных:
для записи основных данных:
Таблица 8
| Признаки | А (да) | А (нет) | Итого |
| В (да) | a | b | a + b |
| В (нет) | c | d | c +d |
| Итого | a + c | b + d |
В таблице под а, b, c, d понимается числовое распределение единиц по определенным показателям
Например. Нужно оценить наличие связи между работниками торговли, распределёнными по полу и содержанию работы. Для этой цели был проведён анализ «Исследование социальных аспектов трудовой деятельности работников торговых предприятий». Результаты исследования были помещены в статистическую таблицу.
Таблица
| Работа | Мужчины | Женщины | Всего |
| Интересная | 300(а) | 201(b) | 501(a+b) |
| Неинтересная | 130(с) | 252(d) | 381(c+d) |
| итого | 430(а+с) | 453(b+d) | 883(a+b+c+d) |
Рассчитаем коэффициент ассоциации:
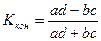 =
= 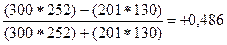
Величина коэффициента в этом примере соответствует среднему размеру связи, несмотря на различие мнений о своей работе мужчин и женщин. Для случаев, когда один из показателей в четырехклеточной таблице отсутствует, необходимо предпочтение отдать коэффициенту контингенции (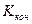 ):
):
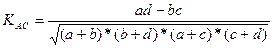 ,
,
Где а, b, с, d, - числа в четырёхклеточной таблице.
Коэффициент контингенции изменяется от +1 до -1, но всегда меньше коэффициента ассоциации. Проверим это утверждение по тем же данным:
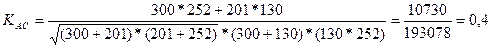
Коэффициенты находятся близко друг от друга и подтверждают предположение о положительной, но не очень тесной связи между показателями.
На практике чаще используют следующие непараметрические показатели связи (коэффициенты), отражающие взаимосвязь между признаками.
Коэффициент Фехнера определяется по формуле:
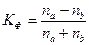 , где
, где
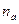 – количество совпадений по знакам в отклонениях между факторным признаком (х) и результативным (у). Данные отклонения находятся путем вычитания из варианта групповой средней (по каждой единице для всей совокупности). Совпадением считается “+” и “+” в отклонения (х) у факторного и результативного признака по отдельной единице (или “-“ и “-“ или “ без отклонения в факторном и результативном признаке).
– количество совпадений по знакам в отклонениях между факторным признаком (х) и результативным (у). Данные отклонения находятся путем вычитания из варианта групповой средней (по каждой единице для всей совокупности). Совпадением считается “+” и “+” в отклонения (х) у факторного и результативного признака по отдельной единице (или “-“ и “-“ или “ без отклонения в факторном и результативном признаке).
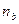 – количество несовпадений.
– количество несовпадений.
Коэффициент Фехнера принимает значения в интервале 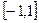 : 0 – отсутствие связи, 1 – полная связь, при этом коэффициент положительная величина при прямой связи, и отрицательная при обратной.
: 0 – отсутствие связи, 1 – полная связь, при этом коэффициент положительная величина при прямой связи, и отрицательная при обратной.
Пример. Имеются данные о з/плате и стаже 15 менеджеров (таб. 12.11). Найдем средний стаж (5,6 лет) и средний заработок (10,9 тыс. руб.). Теперь по каждому человеку будем находить отклонение его варианта стажа и з/пл от средних показателей. (столбцы 4-5).
Таблица 11
| № работника | стаж работы, лет (х) | з/плата, тыс.руб. (у) | 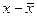 |  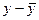 |
| 1 | 2 | 3 | 4 | 5 |
| -0,6 | 1,1 | |||
| 4,4 | 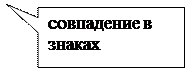 4,1 4,1 | |||
| 7,4 | -3,6 | -3,5 | ||
| 7,8 | -2,6 | -3,1 | ||
| 11,7 | -0,6 | 0,8 | ||
| 3,4 | 2,1 | |||
| 1,4 | 1,1 | |||
| -1,6 | -2,9 | |||
| 0,4 | 1,1 | |||
| -0,6 | 0,1 | |||
| 2,4 | 3,1 | |||
| 14,5 | 3,4 | 3,6 | ||
| -3,6 | -3,9 | |||
| 7,5 | -2,6 | -3,4 | ||
| 10,5 | 0,4 | -0,4 | ||
| итого | 163,4 | |||
| среднее | 5,6 | 10,9 |
У первого работника стаж ниже среднего на -0,6 лет, а зарплата выше среднего на 1,1тыс. руб. – это несовпадение отклонений от средней по факторному и результативному признаку (т.е. это составляющая 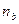 ). Такие же несовпадения встречаются у 5, 10, 15 работника. Всего людей с несовпадением отклонений 4 чел.
). Такие же несовпадения встречаются у 5, 10, 15 работника. Всего людей с несовпадением отклонений 4 чел.
У второго работника стаж работы выше среднего и зарплата больше среднего. Это совпадение отклонений. Это составляющая 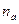 . Всего таких людей 11.
. Всего таких людей 11.
Найдем коэффициент Фехнера:
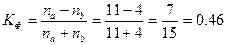 Данный коэффициент показывает, что связь между признаками существует, но она несущественная, хотя и положительная (т.е. с увеличением стажа растет з/плата).
Данный коэффициент показывает, что связь между признаками существует, но она несущественная, хотя и положительная (т.е. с увеличением стажа растет з/плата).
Этот коэффициент используют при небольшом количестве исследуемых единиц.
Коэффициент ранговой корреляции Спирмена. Используется для ранжированных данных. Ранги – порядковые номера единиц совокупности в ранжированном ряду. Ранжировать оба признака необходимо в одном и том же порядке от меньших к большим или наоборот. Рассчитывается коэффициент по формуле:
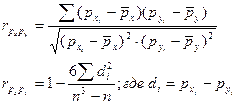
где 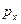 и
и 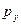 ранги единиц совокупности,
ранги единиц совокупности,
di – разность между рангами факторного и результативного признака по каждой единице совокупности,
п - число наблюдений или изучаемых единиц, соответствует количеству рангов.
Коэффициент корреляции рангов принимает значения в интервале 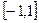 : 0 – отсутствие связи, 1 – полная связь, при этом коэффициент положительная величина при прямой связи, и отрицательная при обратной. Пример. Рассчитаем этот коэффициент для данных из предыдущего примера. Расчеты удобно оформить в следующей таблице:
: 0 – отсутствие связи, 1 – полная связь, при этом коэффициент положительная величина при прямой связи, и отрицательная при обратной. Пример. Рассчитаем этот коэффициент для данных из предыдущего примера. Расчеты удобно оформить в следующей таблице:
Таблица
| № работника | стаж работы, лет (х) | Ранг по х (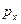 ) ) | з/плата, тыс.руб. (у) | Ранг по y (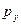 ) ) | 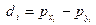 | 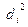 |
| -3 | ||||||
| 7,4 | -1 | |||||
| 7,8 | -1 | |||||
| 11,7 | -1 | |||||
| -2 | ||||||
| -1 | ||||||
| 14,5 | ||||||
| 7,5 | ||||||
| 10,5 | ||||||
| итого |
Работник под № 3 имеет самый маленький стаж работы. Присваиваем ему ранг 1. Такой же стаж имеет и работник №13. Его ранг 2. (Ранги, при равных значениях (х) присваиваются с верхних значений к нижним). Четвертому работнику со стажем 3 года присваиваем ранг 3 и.т.д. Самый большой стаж у работника № 2 – его ранг 15.
После этого присвоим ранги тем же работникам по уровню з/платы (результативный признак). Работник №13 имеет самую низкую з/плату. Следовательно, его ранг по показателю (у) 1. Второй работник имеет з./плату чуть больше, присваиваем ему ранг 2 и т.д. Самая высокая з/плата у работника №2, его ранг по (у) 15. При ранжировании соответствующих значений результативного признака в ряде случаев, обнаруживается равенство величин. В этом случае им присваивают средние ранги.
Затем найдем 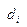 , как разницу между рангами по факторному и результативному признаку. У работника №3 эта разница составит 1-2=-1. У работника №2 разница рангов - 15-15=0 и т.д.
, как разницу между рангами по факторному и результативному признаку. У работника №3 эта разница составит 1-2=-1. У работника №2 разница рангов - 15-15=0 и т.д.
Возведем 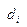 в квадрат и рассчитаем коэффициент корреляции рангов:
в квадрат и рассчитаем коэффициент корреляции рангов:
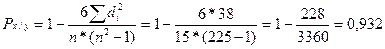 .
.
Данный коэффициент показывает более тесную связь между признаками, чем ранее вычисленный, по формуле Фехнера. Преимуществом ранговых коэффициентов корреляции является то, что ранжировать можно и по описательным признакам, которые нельзя выразить численно. Следовательно, расчет коэффициента Спирмена возможен для следующих пар признаков: кол-во – кол-во; описательный – количественный; описательный – описательный.
Для изучения статистической связи между качественными (атрибутивными) признаками может быть использована аналитическая группировка при наличии более двух возможных значений каждого из взаимосвязанных признаков. Результат группировки представляется в таблице сопряженности  и вычисляются коэффициенты взаимной сопряженности:
и вычисляются коэффициенты взаимной сопряженности:
Коэффициент взаимной сопряженности Пирсона вычисляется по следующей формуле:
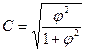
Где 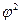 - показатель средней квадратической сопряжённости. Определяется по формуле:
- показатель средней квадратической сопряжённости. Определяется по формуле:
 , где
, где
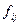 - частоты каждой клетки таблицы сопряженности,
- частоты каждой клетки таблицы сопряженности,
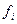 – итоговые частоты по строкам,
– итоговые частоты по строкам,
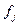 – итоговые частоты по графам.
– итоговые частоты по графам.
Недостаток коэффициента Пирсона в том, что он не достигает единицы и при полной связи признаков, а лишь стремится к единице при увеличении числа групп.
Коэффициент взаимной сопряжённости, предложенный известным статистиком А. А. Чупровым, вычисляется по формуле:
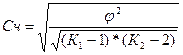
Где К1 - число групп по колонкам;
К2 - число групп по строкам.
Коэффициенты взаимной сопряженности принимают значения в интервале 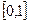 : 0 – отсутствие связи, 1 – полная связь, при этом коэффициент Чупрова дает более осторожную оценку тесноты связи. Результат, полученный по коэффициенту взаимной сопряжённости А.А.Чупрова, более точен, поскольку он учитывает число групп по каждому признаку.
: 0 – отсутствие связи, 1 – полная связь, при этом коэффициент Чупрова дает более осторожную оценку тесноты связи. Результат, полученный по коэффициенту взаимной сопряжённости А.А.Чупрова, более точен, поскольку он учитывает число групп по каждому признаку.
Расчёт коэффициента взаимной сопряжённости производится по следующей схеме:
Таблица 9
| Признаки | Ф | В | С | Итого |
| D | ƒ11 | ƒ12 | ƒ13 | ƒ1i |
| E | ƒ21 | ƒ22 | ƒ23 | ƒ2i |
| F | ƒ31 | ƒ32 | ƒ33 | ƒ3i |
| Итого | ƒ1j | ƒ2j | ƒ3j | n |
в таблице
ƒij - частоты взаимного сочетания двух атрибутивных признаков,
n – число пар наблюдений.
Пример. Имеются данные о посещаемости занятий и успеваемости студентов (таблица). Найдем коэффициенты взаимной сопряженности на примере взаимосвязи между посещением занятий и успеваемостью студентов.
Таблица
| Посещение занятий | Успеваемость | Итого | ||
| Отличная | Средняя | Неудовлетворительная | ||
| Пропуски отсутствуют | ||||
| Немного пропусков | ||||
| Частое отсутствие на занятиях | ||||
| Итого |
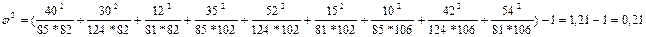 .
.
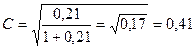 - средняя положительная взаимосвязь.
- средняя положительная взаимосвязь.
Коэффициент взаимной сопряжённости Чупрова:
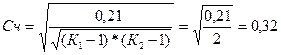
Коэффициент Чупрова показывает наличие взаимосвязи между посещаемостью и успеваемостью студентов. Эта связь положительная, но не сильная.
 2014-02-17
2014-02-17 1511
1511