На множестве всех линейных преобразований пространства V расмотрим операции:
1. Умножение на число: 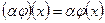 .
.
2. Сложение (вычитание) 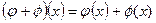
3. Умножение 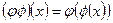 .
.
Легко проверить линейность всех этих преобразований и вывести следующие формулы, связывающие их матрицы
1. 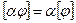
2. 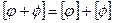
3. 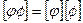
Линейное преобразование, переводящее каждый вектор в себя, называется тождественным преобразованием и обозначается 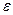 . В любом базисе матрица тождественного преобразования равна единичной.
. В любом базисе матрица тождественного преобразования равна единичной.
Пусть 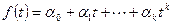 - некоторый многочлен,
- некоторый многочлен, 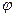 - линейное преобразование пространства V. Сопоставим многочлену
- линейное преобразование пространства V. Сопоставим многочлену 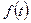 линейное преобразование
линейное преобразование 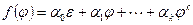 . Будем говорить, что преобразование
. Будем говорить, что преобразование 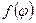 получено подстановкой
получено подстановкой 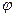 в многочлен
в многочлен 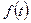 . Матрица
. Матрица 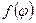 может быть вычислена по формуле
может быть вычислена по формуле 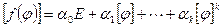 .
.
Свойство 7.1. Пусть 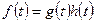 . Тогда
. Тогда 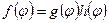 .
.
 2014-02-17
2014-02-17 708
708








