1. Каждая единица генеральной совокупности должна иметь равные возможности попасть в выборку.
2. Количество единиц в выборке должно быть достаточно большим.
Основная задача выборочного наблюдения в экономике состоит в том, чтобы на основе характеристик выборочной совокупности (средней и доли) получить достоверное суждение о показателях средней и доли в генеральной совокупности.
При любом статистическом наблюдении возникают ошибки двух видов:
1) ошибки регистрации:
– случайные;
– систематические;
2) ошибки репрезентативности (представительности):
– случайные;
– систематические.
Ошибки репрезентативности присущи только выборочному наблюдению и возникают в силу того, что выборочная совокупность не полно воспроизводит генеральную. Они представляют собой расхождение между значениями показателей, полученных по выборке, и значениями этих величин, которые были бы получены при сплошном наблюдении, т. е. между величиной выборочных и соответствующих генеральных показателей.
Значения ошибки репрезентативности зависят от вида, метода и способа формирования выборочной совокупности.
По виду различают индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности. При групповом отборе – качественно-однородные группы или серии изучаемых единиц. Комбинированный отбор предполагает сочетание первых двух.
По степени охвата единиц совокупности различают большие и малые (когда число отобранных единиц меньше 30) выборки.
Таблица 8.1
Условные обозначения
| Показатель | Выборочная совокупность | Генеральная совокупность |
| Средняя | 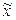
| 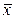
|
| Дисперсия | σ² | S² |
| Доля единиц, обладающих признаком | W | p |
| Численность единиц | n | N |
Выборочная доля или частость определяются отношением числа единиц, обладающих изучаемым признаком m, к общему числу единиц выборочной совокупности n:
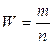 .
.
Выборочная средняя и выборочная доля являются случайными величинами, которые могут принимать различные значения в зависимости от того, какие единицы совокупности попали в выборку. Поэтому ошибки выборки тоже являются случайными величинами и могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок выборки – среднюю ошибку выборки (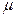 ).
).
Возможные расхождения между характеристиками генеральной и выборочной совокупностей измеряются средней ошибкой выборки 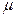 . Она зависит:
. Она зависит:
– от объема выборки (чем больше численность выборки, тем меньше величина средней ошибки выборки);
– от степени варьирования изучаемого признака (степень варьирования характеризуется дисперсией) – чем меньше вариация признака, тем меньше средняя ошибка выборки.
При нулевой дисперсии (признак не варьирует) средняя ошибка выборки 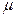 = 0, т. е. любая единица генеральной совокупности будет точно характеризовать всю совокупность по этому признаку.
= 0, т. е. любая единица генеральной совокупности будет точно характеризовать всю совокупность по этому признаку.
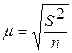 .
.
Учитывая, что дисперсию генеральной совокупности (S2) иногда невозможно или нецелесообразно определить, в практике её заменяют выборочной дисперсией (σ²) с применением специального коэффициента 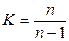 , тогда
, тогда 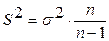 и средняя ошибка выборки
и средняя ошибка выборки 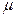 будет вычисляться по формуле
будет вычисляться по формуле 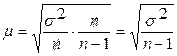 (такая замена применяется в случае малой выборки n < 30).
(такая замена применяется в случае малой выборки n < 30).
Так как коэффициент К при достаточно больших n – величина близкая к 1
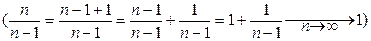 , то можно принять σ² ≈ S², т. е.
, то можно принять σ² ≈ S², т. е.
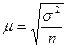 (только для больших выборок).
(только для больших выборок).
Для среднего значения признака в генеральной совокупности имеем следующую оценку: 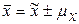 или
или 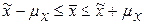 , а для доли единиц, обладающих признаком в генеральной совокупности:
, а для доли единиц, обладающих признаком в генеральной совокупности: 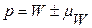 или
или 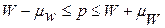 .
.
Но такое суждение можно гарантировать не с абсолютной достоверностью, а лишь с определенной степенью вероятности, равной 0,683.
В математической статистике доказывается, что о величине средней ошибки можно судить с постоянной степенью вероятности 0,683, т. е. из 1000 выборочных обследований в 683 случаях сводные показатели генеральной совокупности будут отличаться от сводных показателей выборочной совокупности не более чем на величину средней ошибки выборки (μ), а в остальных 317 случаях они могут выйти за эти пределы.
Чтобы повысить вероятность суждения, необходимо расширить пределы отклонений выборочной средней от генеральной (и выборочной доли от генеральной) путем увеличения средней ошибки в t раз.
Получаем новую ошибку:
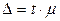 ,
,
где 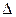 – предельная ошибка выборки;
– предельная ошибка выборки;
t – нормированное отклонение, или «коэффициент доверия», зависящий от вероятности с которой гарантируется предельная ошибка.
Значения вероятности при различных значениях t определяют на основе специально составленных таблиц. Приведем некоторые значения, применяемые наиболее часто для выборок достаточно большого объема, где n 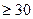 :
:
Таблица 8.2
| t | 1,5 | 1,96 | 2,5 | 2,580 | |||
| P - вероятность | 0,683 | 0,866 | 0,950 | 0,954 | 0,988 | 0,990 | 0,997 |
Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы.
Интервальная оценка:
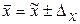 или
или 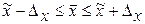 ;
;
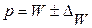 или
или 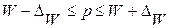 .
.
Величина ошибок зависит от способа отбора единиц в выборку.
 2014-02-17
2014-02-17 956
956








