Необходимые и достаточные условия существования наклонной асимптоты.
Пусть функция f(x) определена в О(+¥) и
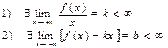
тогда прямая y=kx+b правая наклонная асимптота
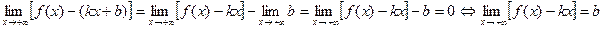
Замечание: если условие 1) не выполнено, то нужно посчитать предел lim(f(x)), чтобы выяснить поведение
х®+¥
функции на бесконечности.
1) Область определения
2) Симметрия и периодичность
3) Вертикальные асимптоты
4) Наклонные асимптоты
5) Критические точки, если есть, то находим точки экстремума и промежутки возрастания и убывания функции f'(x)=0 или f’(x) не существует, а f(x) существует
6) Возможные точки перегиба f’’(x)=0, либо f’’(x) не существует, но f’(x) существует следовательно промежутки выпуклости и вогнутости
7) Точки пересечения с осями координат и промежутки знака постоянства (если можно)
Пример:
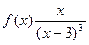
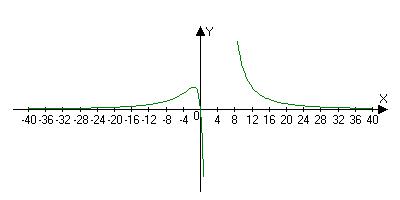
1) Область определения D: x¹3
2) Функция не симметрична и не периодична
3) 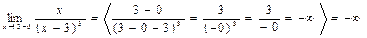
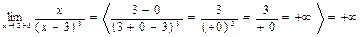
Þ х=3 правая и левая вертикальная асимптота
4) 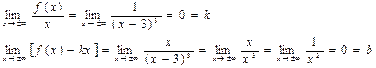
Þ y=0 правая и левая горизонтальная асимптота
5)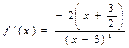
критическая точка х1=-3/2

f(-3/2)=4/243
6)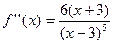
критическая точка х2=-3

f(-3)=1/72
7)x=0 y=0
Приближенные методы решения уравнения f(x)=0
1) Метод хорд
а) f(x), f’(x), f’’(x) – непрерывны на отрезке [a,b]
б) f(a)f(b)<0
в) f’(x) и f’’(x) – сохраняют знаки на отрезке [a,b]
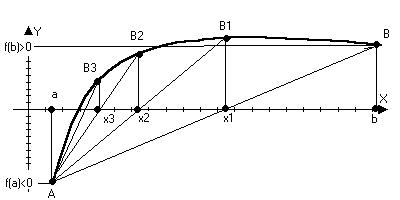
f(x)=0;A(a;(f(a)),B(b;f(b))
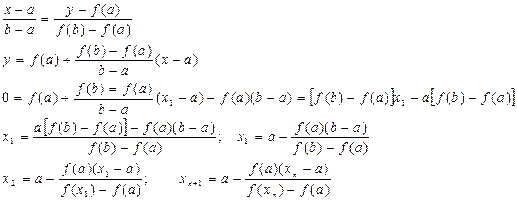
 2014-02-18
2014-02-18 461
461








