2014-02-18
837
Во многих случаях представляет интерес вопрос о том, какова статистическая связь между двумя стационарными случайными процессами X(t) и Y(t). Принято вводить взаимные функции корреляции этих процессов по формулам:
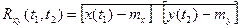
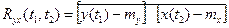(6.17)
Случайные процессы называются стационарно связанными, если функци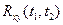и 
и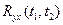 
, зависят не от самих аргументов 
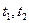, а лишь от разности 
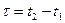. В этом случае, очевидно,
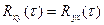(6.18)
Предположим, что случайные процессы X(t) и Y(t) статистически независимы, в том смысле, что для мгновенных значени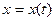й 
и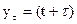 
независимо от величины 
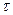двумерная совместная плотность вероятности 
.
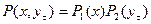Тогда:
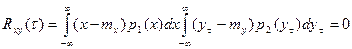
То есть из статистической независимости случайных процессов вытекает их некоррелированность. Однако в общем случае обратное утверждение не справедливо.
