Дифференциальные уравнения (обыкновенные)
Способы математического описания АСР
Основы теории автоматического регулирования
Динамические характеристики элементов АСР описываются 2-мя способами: 1) Дифференциальные уравнения 2) Передаточные функции
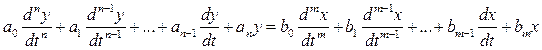
у - выходная переменная АСР, х - входная, dt - динамика АСР. Для решения уравнения применяют операционное исчисление основанные на преобразовании Лапласа.
Преобразование Лапласа имеет следующий вид
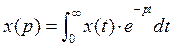 гдн
гдн 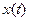 - аргумент,
- аргумент, 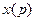 - изображение данного аргумента,
- изображение данного аргумента, 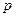 - некоторая переменная которая называется переменная Лапласа
- некоторая переменная которая называется переменная Лапласа
Свойства преобразования при начальных нулевых значениях т.е. t=0 x(t)=0
1)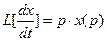 ,
, 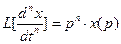 , 2)
, 2) 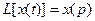 , 3)
, 3) 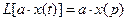 ,
, 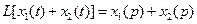 , 4)
, 4) 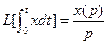 , где L-преобразование
, где L-преобразование
Преобразование по Лапласу с использованием его свойств
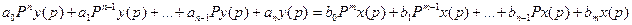 возьмем отношение
возьмем отношение 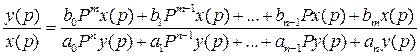
Отношение преобразуем по Лапласу выходной величины АСР или линейно к преобразованной по Лапласу входной величины элемента называется передаточной функцией АСР или элемента. Знаменатель передаточной функции = 0, называется характеристическим уравнением АСР 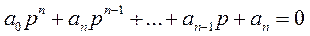
 2014-02-18
2014-02-18 443
443








