Предпочтения

Если для потребителя набор 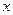не хуже, чем набор 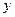, то будем говорить, что данный потребитель нестрого предпочитает набор 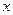набору 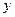и записывать .

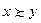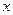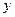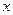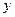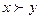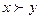
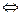
Если для потребителя набор лучше, чем набор , то будем говорить, что данный потребитель строго предпочитает набор набору и записывать . По определению 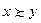и не верно, что .

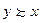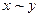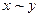
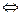
Запись означает, что наборы эквивалентны: 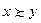и .

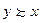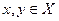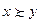Аксиома полноты: Для любых наборов либо , либо 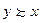(либо и то и другое).

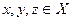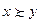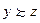Аксиома транзитивности. Для любых наборов , если и , то .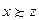

Предпочтения, удовлетворяющие аксиомам полноты и транзитивности, называются рациональными.

Аксиома строгой монотонности. Для любых наборов 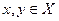, есл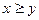и и 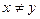(т.е. в наборе 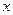каждого блага не меньше, чем в наборе 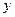, и хотя бы одного строго больше), то .

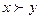Аксиома (строгой) выпуклости, если для любого 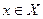множество наборов не хуже 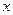(строго) выпукло.

Кривая безразличия, проходящая через точку 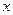- это множество наборов 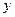, эквивалентных набору 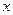: 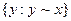.Если предпочтения рациональны, то кривые безразличия не пересекаются.

Предельная норма замещения второго блага первым 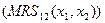– максимальное количество второго блага, от которого готов отказаться потребитель, чтобы увеличить потребление первого блага на малую величину; это наклон кривой безразличия в точке 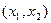по абсолютной величине.

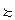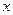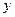Функцией полезности, представляющей предпочтения , определенные на множестве X, называют функцию u: X→R такую, что для любых наборов и из 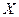соотношение 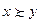имеет место тогда и только тогда, когда .

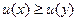Утверждение: Если предпочтения представимы с помощью функции полезности, то эти предпочтения являются рациональными.