2014-02-18
417План
Темы: Монополия. Стратегические взаимодействия: олигополия
- Монополия: монополия и совершенная конкуренция, неэффективность монополии; чистые потери от монополии.
- Олигополия: модель Курно.
1. Монополия.
Утверждение. Пусть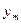 
- равновесный уровень выпуска монополиста, а 
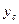- равновесный уровень выпуска при совершенной конкуренции (т.е. объем выпуска, который был бы выбран фирмой с такой же функцией издержек, но принимающей цену заданной). Тогда, если обратная функция спроса, 
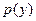, убывает, то
(1)
;
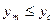(2) если кроме того обратная функция спроса и функция издержек дифференцируемы,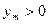 
и 
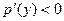, то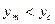 
.
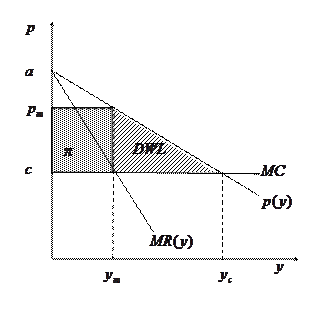
Равновесный уровень выпуска при монополии неэффективен (не Парето-оптимален),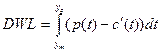 
(deadweight loss) - чистые потери от монополии, мера снижения благосостояния потребителей в результате того, что они платят не конкурентную, а монопольную цену.
Пример. Пусть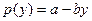 
, 
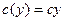, причем 
, 
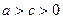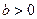. Равновесная цена при совершенной конкуренции определяется из условия равенства предельным издержкам: 
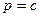, соответственно, равновесный уровень выпуска при совершенной конкуренции (он же и будет эффективным) будет следующим: 
.
|
|
|
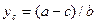Равновесный уровень выпуска при монополии, 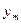, будет положительным, поскольку выполнены все предпосылки соответствующего утверждения: если обратная функция спроса 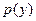и функция издержек 
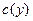дифференцируемы и 
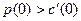, то 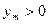(см. план лекции 8), и определяется из условия 
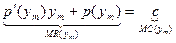, откуда находим 
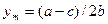, что в два раза меньше оптимального. Соответственно, равновесная цена составит 
.
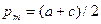Чистые потери от монополии:
.
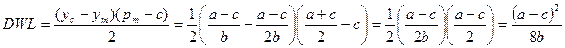2. Олигополия.
Модели некооперативного поведения олигополистов:
| Одновременно | Последовательно | |
| Количество (выпуск) | Модель Курно | Модель Штакельберга |
| Цена | Модель Бертрана | Ценовое лидерство |
Будем считать, что некоторую однородную продукцию производят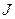 
фирм технологии которых представлены возрастающими выпуклыми функциями издержек 
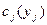, а спрос на продукцию задается убывающей обратной функцией совокупного спроса 
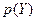, где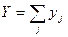 
, 
.
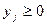Модель Курно (дуополия): фирмы одновременно и независимо выбирают уровень выпуска. Пусть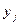 
- это выпуск фирмы 
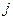, а через 
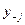обозначим выпуск другой фирмы (или совокупный выпуск всех других фирм, если их больше двух). Задача фирмы 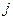имеет вид: 
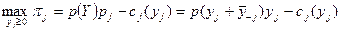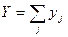, где и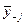 
- ожидаемый выпуск фирмы-конкурента (и в равновесии ожидания оправдываются). Обозначим решение этой задачи через 
.
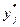Определение: Набор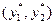 
составляет равновесие в модели дуополии Курно (равновесие по Нэшу), если для любой фирмы 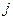, 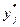является решением задачи фирмы 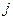при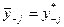 
.
Зависимость оптимального объема производства 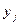от 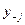называют функцией (отображением в общем случае) реакции: 
.
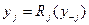Если оптимальный отклик однозначен, то равновесие Курно 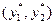является решением системы: 
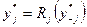, где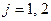 
. Графически, равновесие в модели Курно характеризуется пересечением кривых реакции в пространстве выпусков.
|
|
|
