Классический способ нахождения вероятности
Классификация событий
Рассмотрим простейший пример, который мы будем изучать с разных сторон в следующих двух параграфах первой лекции.
________________________
Пример № 1. Бросили игральную (шестигранную) кость (один раз). Найти вероятность того, что выпадет: 1) «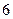 »; 2) чётное число; 3) нечётное число; 4) число, меньшее «
»; 2) чётное число; 3) нечётное число; 4) число, меньшее «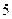 ».
».
Прелюдия к решению. Рассмотрим следующие элементарные события (возможно, на их основе представим нужные нам события):
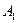 - бросили игральную кость и выпала «
- бросили игральную кость и выпала «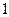 »;
»;
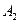 - бросили игральную кость и выпала «
- бросили игральную кость и выпала «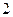 »;
»;
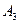 - бросили игральную кость и выпала «
- бросили игральную кость и выпала «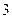 »;
»;
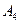 - бросили игральную кость и выпала «
- бросили игральную кость и выпала «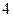 »;
»;
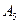 - бросили игральную кость и выпала «
- бросили игральную кость и выпала «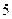 »;
»;
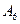 - бросили игральную кость и выпала «
- бросили игральную кость и выпала «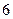 ».
».
Теперь легко представить, что:
1) событие 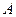 , состоящее в том, что бросили игральную кость и выпала «
, состоящее в том, что бросили игральную кость и выпала «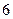 », есть событие
», есть событие 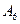 , т.е.
, т.е.
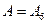 ;
;
2) событие 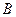 , состоящее в том, что бросили игральную кость, а выпало чётное число, представляет собой множество, состоящее из трёх событий,
, состоящее в том, что бросили игральную кость, а выпало чётное число, представляет собой множество, состоящее из трёх событий,
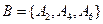 ;
;
3) событие 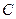 , состоящее в том, что бросили игральную кость, а выпало нечётное число, представляет собой множество, состоящее из трёх событий,
, состоящее в том, что бросили игральную кость, а выпало нечётное число, представляет собой множество, состоящее из трёх событий,
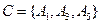 ;
;
4) событие 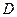 , состоящее в том, что бросили игральную кость, а выпало число, меньшее «
, состоящее в том, что бросили игральную кость, а выпало число, меньшее «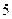 », представляет собой множество, состоящее из четырёх событий,
», представляет собой множество, состоящее из четырёх событий,
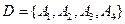 .
.
_________________________
Чтобы научиться находить вероятности сложных событий, нужно провести их классификацию и научиться проводить операции над ними.
Определение. Сумма 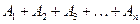 конечного числа событий
конечного числа событий 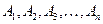 – событие, состоящее в наступлении хотя бы одного из них.
– событие, состоящее в наступлении хотя бы одного из них.
_________________________
Пример. В примере № 1 событие 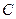 равно сумме событий
равно сумме событий 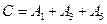 .
.
Определение. Произведение 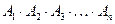 конечного числа событий
конечного числа событий 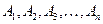 – событие, состоящее в наступлении всех этих событий.
– событие, состоящее в наступлении всех этих событий.
________________________
Пример. В примере № 1 событие 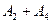 есть произведение событий
есть произведение событий 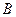 и
и 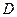 :
: 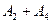
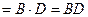 (математики экономят на знаке произведения).
(математики экономят на знаке произведения).
________________________
Определение. Противоположным событием 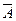 называется событие, состоящее в не появлении события
называется событие, состоящее в не появлении события 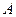 .
.
________________________
Пример. В примере № 1 событие 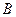 есть противоположное к событию
есть противоположное к событию 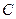 :
: 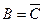 .
.
________________________
Рассмотрим важные для дальнейшего понятия.
Определение. Два события называются несовместными, если наступление одного из них исключает возможность наступления другого. В противоположном случае события называются совместными.
________________________
Пример. В примере № 1 события 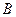 и
и 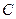 - несовместные, а события
- несовместные, а события 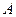 и
и 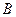 - совместные.
- совместные.
________________________
Определение. События называются равновозможными (равновероятными), если вероятность наступления каждого из них одна и та же.
________________________
Пример. В примере № 1 события 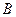 и
и 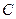 являются равновозможными, если кость сделана без изъянов. Также следует признать равновозможными и события
являются равновозможными, если кость сделана без изъянов. Также следует признать равновозможными и события 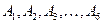 .
.
________________________
Определение. События называются элементарными, если их наступление нельзя связать с наступлением других событий в этом опыте.
________________________
Пример. Извлечение карты «Дама пик» из перемешанной колоды карт – событие элементарное.
________________________
Определение. События называются сложными, если их наступление в опыте можно связать с наступлением других событий в этом опыте.
________________________
Пример. Извлечение «пиковой карты» из перемешанной колоды карт – событие сложное, так как его наступление связано с рядом событий в этом опыте, а именно, извлечение «Туз пик», «Король пик», …
_______________________
Определение. События образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное (отличное от входящих в группу) событие.
Пример. В примере № 1 события 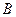 и
и 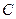 образуют такую полную группу, если не учитывать, что кость при бросании может встать на ребро, исчезнуть (провалиться под пол), …
образуют такую полную группу, если не учитывать, что кость при бросании может встать на ребро, исчезнуть (провалиться под пол), …
________________________
Определение. Событие называется достоверным, если оно не может не произойти в условиях данного опыта.
Вероятность достоверного события равна 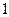 , т.к. для этого события
, т.к. для этого события 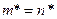 (напомним, что
(напомним, что 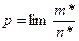 ).
).
________________________
Пример. В примере № 1 событие 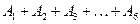 есть как раз такое достоверное событие.
есть как раз такое достоверное событие.
________________________
Определение. Событие, которое не может произойти в условиях данного опыта, называется невозможным событием.
Вероятность невозможного события равна 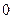 , т.к. для этого события
, т.к. для этого события 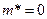 (а
(а 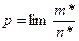 ).
).
________________________
Пример. В примере № 1 событие, равное произведению двух событий 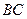 , является как раз невозможным событием. Невозможное событие представляет собой и событие, состоящее в выпадении
, является как раз невозможным событием. Невозможное событие представляет собой и событие, состоящее в выпадении 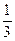 .
.
Пусть мы имеем полную группу равновозможных, несовместных, случайных событий.
Определение. Событие (из такой группы)называется благоприятствующим появлению события 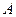 , если появление этого события (из такой группы)влечёт за собой появление события
, если появление этого события (из такой группы)влечёт за собой появление события 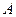 .
.
________________________
Пример. В примере № 1 событие 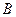 , выпало чётное число при бросании один раз игральной кости, имеет в качестве благоприятствующих событий, следующие события:
, выпало чётное число при бросании один раз игральной кости, имеет в качестве благоприятствующих событий, следующие события: 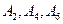 .
.
________________________
Собственно сам классическийспособ нахождения вероятности заключается в следующем (а как может быть по-другому?) простом соображении.
Вероятность события 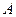 равна отношению числа
равна отношению числа 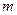 благоприятствующих случайных событий к числу всех возможных случайных событий
благоприятствующих случайных событий к числу всех возможных случайных событий 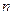 , образующих полную группу равновозможных несовместных событий:
, образующих полную группу равновозможных несовместных событий:
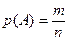 .
.
Исходя из приведённого правила, можно опять установить, что для событий, входящих в состав полной группы равновозможных несовместных событий, имеет место два свойства вероятности:
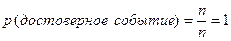 ,
,
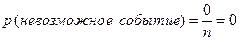 .
.
Теперь можно вернуться к примеру № 1 и предложить окончательное его решение.
________________________
Пример. В примере № 1 полную группу равновозможных несовместных событий составляют события 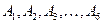 , т.к.:
, т.к.:
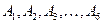 образуют полную группу (об этом мы уже говорили),
образуют полную группу (об этом мы уже говорили),
понятно, что все эти события равновероятны (если кость сделана без изъянов),
понятно, что все эти события несовместны (если кость при бросании не упадёт на ребро). Поэтому 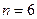 .
.
Тогда событие 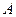 , состоящее в том, что бросили игральную кость и выпала «
, состоящее в том, что бросили игральную кость и выпала «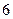 », имеет вероятность:
», имеет вероятность:
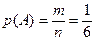 ,
,
т.к. благоприятствующим событием является лишь событие 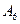 , т.е.
, т.е. 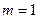 .
.
Событие 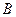 , состоящее в том, что бросили игральную кость, а выпало чётное число, имеет вероятность:
, состоящее в том, что бросили игральную кость, а выпало чётное число, имеет вероятность:
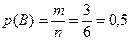 ,
,
т.к. благоприятствующими событиями являются события 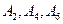 , т.е.
, т.е. 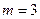 .
.
Событие 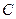 , состоящее в том, что бросили игральную кость, а выпало нечётное число, имеет вероятность:
, состоящее в том, что бросили игральную кость, а выпало нечётное число, имеет вероятность:
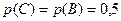 ,
,
о чём мы уже говорили.
Событие 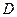 , состоящее в том, что бросили игральную кость, а выпало число, меньшее «
, состоящее в том, что бросили игральную кость, а выпало число, меньшее «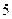 », имеет вероятность:
», имеет вероятность:
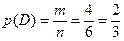 ,
,
т.к. благоприятствующими событиями являются события 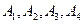 , т.е.
, т.е. 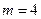 .
.
Пусть в опыте мы имеем полную группу равновозможныхслучайных событий 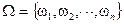 . Если при этом события
. Если при этом события 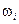 являются элементарными, то такую группу событий называют пространством элементарных событий. Любое сложное событие
являются элементарными, то такую группу событий называют пространством элементарных событий. Любое сложное событие  в опыте всегда связано с рядом элементарных событий из
в опыте всегда связано с рядом элементарных событий из  , которые являются благоприятствующими для его наступления
, которые являются благоприятствующими для его наступления 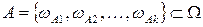 . Тогда элементарное событие может быть изображено графически точкой в пространстве
. Тогда элементарное событие может быть изображено графически точкой в пространстве 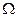 , а сложное событие множеством
, а сложное событие множеством 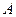 в пространстве
в пространстве 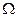 [1-4]. Такое изображение событий представляется диаграммой Эйлера-Вена на рис.1.1.
[1-4]. Такое изображение событий представляется диаграммой Эйлера-Вена на рис.1.1.
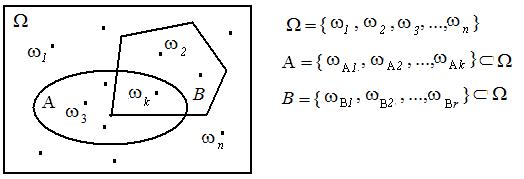
Рис.1.1. Диаграмма Эйлера-Вена для интерпретации событий в пространстве элементарных событий и операций над событиями
Такая интерпретация события, как множества в пространстве событий, позволяет легко и наглядно изображать события, операции над событиями как операции над множествами, понять соотношения алгебры событий:
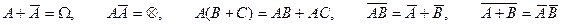 .
.
Если под массой (модулем) события 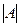 понимать число, характеризующее количество благоприятствующих элементарных исходов, то классический способ вычисления вероятности интерпретируется как отношение массы события к массе пространства:
понимать число, характеризующее количество благоприятствующих элементарных исходов, то классический способ вычисления вероятности интерпретируется как отношение массы события к массе пространства:
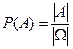 .
.
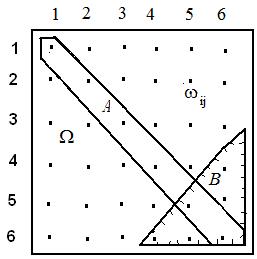 Пример. Пусть в опыте бросаются две игральные кости. Событие
Пример. Пусть в опыте бросаются две игральные кости. Событие 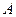 состоит в выпадении дубля, а событие
состоит в выпадении дубля, а событие 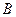 - в выпадении суммы очков на обеих костях не менее 10. Эти события изображены на рис. 1.2. множествами, где точками изображаются элементарные исходы
- в выпадении суммы очков на обеих костях не менее 10. Эти события изображены на рис. 1.2. множествами, где точками изображаются элементарные исходы  , тогда:
, тогда:

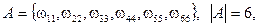
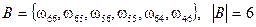 ,
,
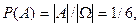
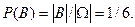
Рис.1.2. Изображение событий
А и B впространстве
 2014-02-18
2014-02-18 1591
1591