Другие виды средних величин

Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака. Различают среднюю гармоническую простую и взвешенную.

Средняя гармоническая простая (the simple harmonic mean).

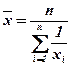
Средняя гармоническая взвешенная (the weighted harmonic mean) применяется тогда, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение.

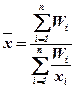
Средняя арифметическая и средняя гармоническая величины могут применятся в одних и тех же ситуациях, но по разным данным. Если в логической формуле неизвестен числитель, то в расчетах применяется средняя арифметическая величина. Если в логической формуле неизвестен знаменатель, то в расчетах используется средняя гармоническая величина.

Средняя квадратическая величина (the quadratic mean) применяется тогда, когда вместо индивидуальных значений признака представлены квадраты исходных величин.

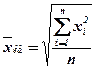
Средняя геометрическая (the geometric mean) применяется в случаях определения средней по значениям, имеющим большой разброс, либо в случаях определения средней величины по относительным показателям.

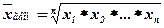
Средняя степенная. В математической статистике различные средние выводятся из формул степенной средней:

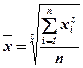
При z = 1 – средняя арифметическая;

z = –1 – средняя гармоническая;

z = 2 – средняя квадратическая.

Чем выше z, тем больше значения средней величины.