2014-02-18
1215
Отыскание параметров выборочного уравнения прямой
Для определения параметров уравнения прямой линии регрессии Y на X была получена система уравнений
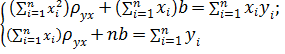(3)
Для простоты записи опустим индексы
(3a)
При выводе этой системы предполагалось, что значения X и соответствующие им значения Y встречались по одному разу. Если дана корреляционная таблица, то до применения системы (3а) предварительно заметим, что из раннее выведенных формул
=
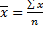
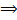
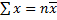
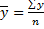
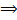
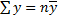
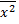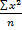
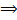
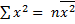
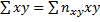(учтено, что пара чисел 
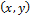наблюдалась 
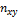раз).
Подставив правые части тождеств в систему (3а) получим:
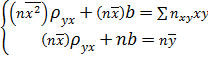(4)
Из второго уравнения найдём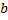 
, предварительно сократив на 
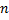, и подставим в уравнение 
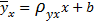, получим
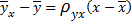. (5)
Для определения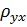 
второе уравнение умножим на 
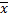и вычтем из первого:
.
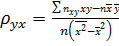Учитывая, что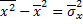 
, получим 
.
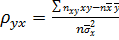Умножим обе части равенства на дробь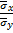 
:
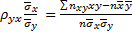(6).
Обозначим правую часть равенства (6) через
тогда равенство (6) примет вид
Откуда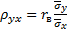 
. Подставив значение 
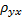в (5), окончательно получим выборочное уравнение прямой линии регрессии Y на X:
где - выборочный коэффициент корреляции.
|
|
|
Если величины Y и X независимы, то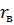 
=0; если связаны линейной функциональной зависимостью, то 
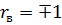. Отсюда следует, что 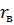измеряет тесноту линейной связи между Y и X.
