Корреляционный момент и коэффициент корреляции

Определение 9.10. Корреляционным моментом системы двух случайных величин называется второй смешанный центральный момент:

K_xy = μ_1,1 = M ((X – M (X))(Y – M (Y))).(9.8)

Для дискретных случайных величин 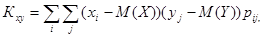для непрерывных случайных величин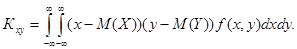

Безразмерной характеристикой коррелированности двух случайных величин является коэффи-циент корреляции

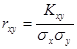. (9.9)

Корреляционный момент описывает связь между составляющими двумерной случайной вели-чины. Действительно, убедимся, что для независимых Х и Y K_xy = 0. В этом случае f (x,y) = =f ₁(x) f ₂(y), тогда

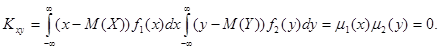
Итак, две независимые случайные величины являются и некоррелированными. Однако понятия коррелированности и зависимости не эквивалентны, а именно, величины могут быть зависимы-ми, но при этом некоррелированными. Дело в том, что коэффициент корреляции характеризует не всякую зависимость, а только линейную. В частности, если Y = aX + b, то r_xy = ±1. Найдем возможные значения коэффициента корреляции.

Теорема 9.1.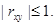

Доказательство. Докажем сначала, что 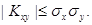Действительно, если рассмотреть случай-ную величину 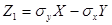и найти ее дисперсию, то получим: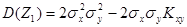. Так как дисперсия всегда неотрицательна, то 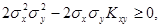откуда 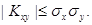Отсюда 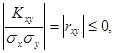что и требовалось доказать.