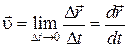 . (1.1)
. (1.1)
Это значит, что вектор скорости 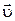 материальной точки в данный момент времени равен производной от радиуса-вектора
материальной точки в данный момент времени равен производной от радиуса-вектора 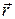 по времени и направлен по касательной к траектории в данной точке в сторону движения (как и вектор
по времени и направлен по касательной к траектории в данной точке в сторону движения (как и вектор 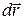 ).
).
Движение точки также характеризуется ускорением 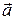 , которое определяет быстроту изменения вектора скорости движения точки со временем
, которое определяет быстроту изменения вектора скорости движения точки со временем
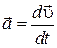 , (1.2)
, (1.2)
т. е. равно производной от вектора скорости по времени. Направление вектора 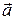 совпадает с направлением приращения
совпадает с направлением приращения 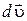 вектора скорости
вектора скорости 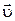 за время dt.
за время dt.
В системе СИ единицами длины, скорости и ускорения являются соответственно метр (м), метр на секунду (м/с) и метр на секунду в квадрате (м/с2).
Из формул (1.1) и (1.2) путем интегрирования можно найти 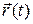 и
и 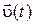
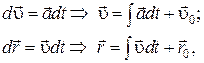
где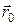 и
и 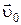 – значения радиуса-вектора и вектора скорости в начальный момент времени t = 0. Эти значения называются начальными условиями.
– значения радиуса-вектора и вектора скорости в начальный момент времени t = 0. Эти значения называются начальными условиями.
Координатный способ.. Радиус-вектор точки в момент времени t можно выразить через эти координаты
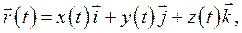 (1.3)
(1.3)
где 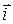 ,
, 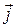 ,
, 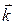 - единичные орты, направленные по осям x, y и z (рис. 1.1).
- единичные орты, направленные по осям x, y и z (рис. 1.1).
Скорость 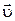 можно выразить через проекции на оси x, y, z
можно выразить через проекции на оси x, y, z
|
|
|
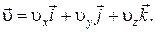 (1.4)
(1.4)
Проекции вектора 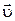 можно выразить через координаты. Для этого продифференцируем выражение (1.3) по времени
можно выразить через координаты. Для этого продифференцируем выражение (1.3) по времени
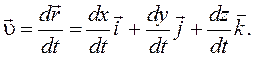 (1.5)
(1.5)
Приравнивая коэффициенты при единичных векторах в формулах (1.3) и (1.5), получим
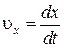 ;
; 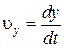 ;
; 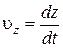 . (1.6)
. (1.6)
Модуль скорости точки
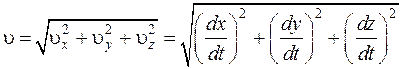 , (1.7)
, (1.7)
Выразим вектор ускорения 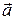 точки через проекции на оси прямоугольной декартовой системы координат
точки через проекции на оси прямоугольной декартовой системы координат
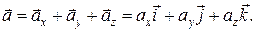 (1.8)
(1.8)
Для проекций ускорения можно получить
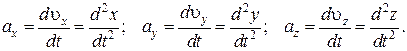 (1.10)
(1.10)
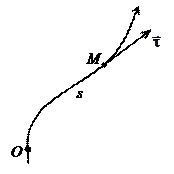 |
Естественный способ. Этот способ применяется, когда известна траектория точки. Положение точки М определяют дуговой координатой s, т. е. расстоянием вдоль траектории от выбранного начала отсчета О (рис. 1.3). При этом произвольно устанавливают положительное направление отсчета координаты s по траектории(указано стрелкой на рисунке).
Рис. 1.3
Движение точки задано, если известны ее траектория, начало отсчета О, положительное направление отсчета дуговой координаты и закон движения точки, т. е. зависимость s (t).
Определим скорость и ускорение точки при естественном способе задания движения. Введем единичный вектор 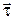 , связанный с движущейся точкой М и направленный по касательной к траектории в сторону возрастания дуговой координаты s (рис. 1.4). Очевидно, что
, связанный с движущейся точкой М и направленный по касательной к траектории в сторону возрастания дуговой координаты s (рис. 1.4). Очевидно, что 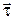 – переменный вектор, т. к. его направление зависит от s. Вектор скорости
– переменный вектор, т. к. его направление зависит от s. Вектор скорости 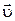 точки М направлен по касательной к траектории, поэтому его можно представить в виде
точки М направлен по касательной к траектории, поэтому его можно представить в виде
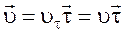 , (1.11)
, (1.11)
 2014-02-18
2014-02-18 1782
1782