2014-02-18
1286
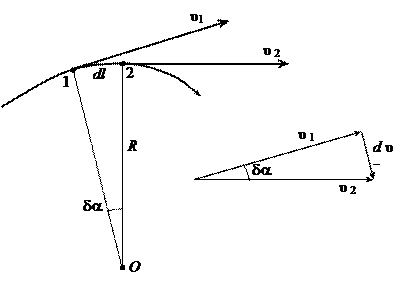
Рис.1.4
 |
Если за малое время dt точка проходит по траектории путь, равный длине элементарной дуги ds, то модуль мгновенной скорости будет равен
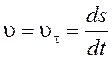, (1.12)
или производной от дуговой координаты s по времени.
Чтобы найти ускорение точки, продифференцируем (1.11) по времени
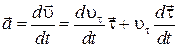. (1.13)
Преобразуем последнее слагаемое этого выражения
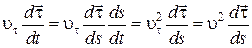. (1.14)
Определим приращение вектора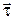 
на участке элементарной дуги ds (рис. 1.4). Можно показать, что при стремлении точки 2 к точке 1 отрезок траектории между ними стремится к дуге окружности с центром в некоторой точке О. Эту точку называют центром кривизны траектории в данной точке, а радиус R соответствующей окружности – радиусом кривизны траектории в той же точке. Как видно из рис. 1.4, угол
,
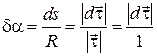откуда
.
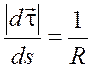Следует учесть, что при ds ® 0 угол между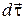 
и 
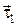стремится к π/2.
Введем единичный вектор 
нормали к траектории в точке 1, перпендикулярный к вектору 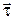в этой точке и направленный к центру кривизны. Запишем последнее равенство в векторном виде
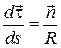. (1.15)
Подставив (1.13) и (1.15) в формулу (1.12), получим
|
|
|
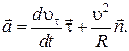
Первое слагаемое в этой формуле называют тангенциальным
ускорением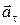 
, а второе – нормальным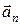 
; 
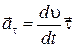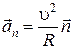. (1.16)
 |
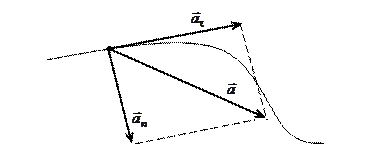Таким образом, полное ускорение
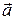точки может быть представлено как векторная сумма тангенциального и нормального ускорений (рис. 1.5). Тангенциальная составляющая описывает изменение скорости по модулю, а нормальная – по направлению.
Рис. 1.5
Модуль полного ускорения точки при движении по криволинейной траектории
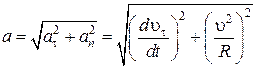. (1.17)
 |
1.3 Вращение вокруг неподвижной оси.
Д вижение твердого тела, при котором две его точки А и В остаются неподвижными, называют вращением тела вокруг неподвижной оси, а неподвижную прямую АВ называют осью вращения тела.
Рассмотрим произвольную точку М тела, не лежащую на оси вращения АВ. При вращении твердого тела расстояния MA, MB и расстояние R от точки М до оси вращения должны оставаться неизменными. Таким образом, все точки тела, вращающегося вокруг неподвижной оси, описывают окружности, центры которых лежат на оси вращения, а плоскости перпендикулярны к этой оси. Вращение Рис.1.5
вокруг неподвижной оси совершают, например, роторы турбин, электрических двигателей и генераторов, коленчатые валы двигателей внутреннего сгорания и т. д.
Найдем элементарное перемещение любой точки А твердого тела при таком повороте. Положение точки А зададим радиусом-векто-
ром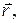 
проведенным из некоторой точки О на оси вращения.
Тогда линейное перемещение конца радиуса-вектора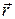 
(рис. 1.6) связано с углом поворота d j соотношением в векторном виде
 |
. (1.18)
Рис. 1.6
Следует отметить, что равенство (1.17) справедливо лишь для бесконечно малого поворота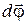 
, в пределах которого радиус-вектор 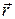можно считать неизменным. Направление этого вектора совпадает с направлением поступательного движения буравчика, рукоятка которого вращается вместе с телом, т. е. подчиняется правилу правого винта.
|
|
|
