Будем считать, что все наблюдения проводятся в одинаковых (равноточных) условиях, т.е. одними и теми же средствами измерения, одним оператором и т.д.
Имеем ряд равноточных измерений: 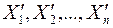 (11)
(11)
Ряд (11) можно назвать многократным измерением, а 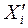 - однократным измерением.
- однократным измерением.
Порядок действий при обработке результатов измерений:
1. Нужно исключить систематическую погрешность:
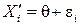 (12)
(12)
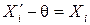 (13)
(13)
Из соотношения (13) следует, что 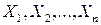 (14) — исправленный ряд измерений.
(14) — исправленный ряд измерений.
2. По исправленным результатам измерений 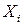 определить их среднее арифметическое значение
определить их среднее арифметическое значение
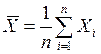 (15)
(15)
Отметим: если известно, что систематическая погрешность во всех наблюдениях оставалась неизменной, то ее можно исключить из  (а не из
(а не из 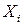 ).
).
Найденное по формуле (15) среднее арифметическое  является состоятельной, несмещенной и эффективной оценкой математического ожидания
является состоятельной, несмещенной и эффективной оценкой математического ожидания 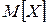 при нормальном распределении результатов наблюдений, а также состоятельной и несмещенной оценкой при любых симметричных (относительно
при нормальном распределении результатов наблюдений, а также состоятельной и несмещенной оценкой при любых симметричных (относительно 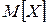 ) распределениях, т.е.
) распределениях, т.е. 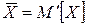 .
.
3. Оценить случайную погрешность каждого отдельного измерения:
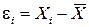 (16)
(16)
Если выполняется условие 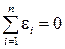 , то пункты 2 и 3 вычислены правильно.
, то пункты 2 и 3 вычислены правильно.
4. Найти СКО однократных измерений:
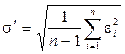 , (17)
, (17)
где 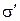 — оценочное значение СКО. Представим (17) в виде
— оценочное значение СКО. Представим (17) в виде
 (18)
(18)
Очевидно, что с увеличением числа наблюдений n возрастает точность оценок  и
и 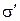 . Разность
. Разность 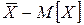 характеризует случайную погрешность определения математического ожидания, т.е. случайную погрешность результата n-кратного измерения. Очевидно, что случайная погрешность также имеет некоторое среднеквадратическое отклонение
характеризует случайную погрешность определения математического ожидания, т.е. случайную погрешность результата n-кратного измерения. Очевидно, что случайная погрешность также имеет некоторое среднеквадратическое отклонение 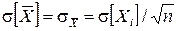 . Его оценка определяется соотношением
. Его оценка определяется соотношением
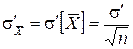 , (19)
, (19)
из которого следует, что результат n-кратного измерения  имеет в
имеет в 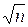 раз меньше СКО по сравнению с результатом единичного измерения
раз меньше СКО по сравнению с результатом единичного измерения 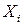 .
.
Оценки СКО единичного и n-кратного измерения называются точечными оценками случайной погрешности. Кроме них используют интервальные оценки погрешности, определяющие границы интервала, внутри которого находятся значения случайной погрешности. При симметричных законах распределения, которые чаще всего имеют место, эти границы располагаются симметрично относительно нулевого значения случайной погрешности. В таких случаях интервал погрешности определяется одним граничным значением 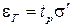 . Таким образом, после вычисления оценки СКО определение интервальной оценки фактически сводится к установлению коэффициента пропорциональности
. Таким образом, после вычисления оценки СКО определение интервальной оценки фактически сводится к установлению коэффициента пропорциональности 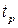 между оценкой СКО
между оценкой СКО 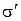 и интервальной оценкой
и интервальной оценкой 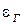 . Однако значение
. Однако значение 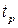 зависит, прежде всего, от закона распределения погрешности. Поэтому выбору коэффициента
зависит, прежде всего, от закона распределения погрешности. Поэтому выбору коэффициента 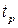 должно предшествовать заключение (или хотя бы обоснованное предположение) об имеющем место законе распределения. По таблице 1 можно определить коэффициент t доверительного или энтропийного интервала погрешности для трех видов ее распределения.
должно предшествовать заключение (или хотя бы обоснованное предположение) об имеющем место законе распределения. По таблице 1 можно определить коэффициент t доверительного или энтропийного интервала погрешности для трех видов ее распределения.
Таблица 1
| Вид распределения | Доверительные значения | Энтропийное значение 
| |
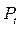
| 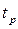
| ||
| Нормальный | 0,9 | 1,64 | 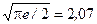
|
| 0,95 | |||
| 0,99 | 2,6 | ||
| 0,997 | |||
| Равномерный | 1,73 | 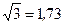
| |
| Треугольный | 2,45 | 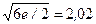
|
При нормальном распределении доверительную вероятность, как правило, принимают равной 0,95. При этом доверительный интервал совпадает с энтропийным интервалом (энтропийным значением) погрешности. В тех случаях, когда измерение нельзя повторить или когда велика цена риска выхода погрешности за пределы интервала (например, если при этом может быть причинен ущерб здоровью), выбирают 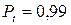 или даже 0,997.
или даже 0,997.
Необходимо отметить, что при малом числе наблюдений 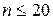 , коэффициент
, коэффициент 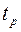 подчиняется распределению Стьюдента (см. табл.2).
подчиняется распределению Стьюдента (см. табл.2).
Таблица 2
| n | 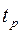
| ||
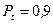
| 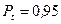
| 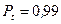
| |
| 2,5 | 3,18 | 5,84 | |
| 2,02 | 2,57 | 4,03 | |
| 1,81 | 2,23 | 3,17 | |
| 1,75 | 2,13 | 2,95 | |
| 1,72 | 2,09 | 2,84 | |
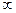
| 1,64 | 1,96 | 2,58 |
Следует иметь в виду, что если среди 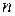 результатов измерений имеются отдельные измерения, резко отличающиеся от остальных в большую или меньшую сторону, прежде всего следует проверить, не являются ли эти результаты
результатов измерений имеются отдельные измерения, резко отличающиеся от остальных в большую или меньшую сторону, прежде всего следует проверить, не являются ли эти результаты 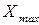 или
или 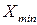 промахами, связанными с опиской, ошибкой в снятии показаний и т. п. Если промахи не установлены, следует проверить, не являются ли эти результаты грубыми погрешностями. Проверка проводится статистическим методом и сводится к сравнению нормированного отклонения
промахами, связанными с опиской, ошибкой в снятии показаний и т. п. Если промахи не установлены, следует проверить, не являются ли эти результаты грубыми погрешностями. Проверка проводится статистическим методом и сводится к сравнению нормированного отклонения 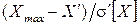 или
или 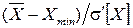 с максимальным маловероятным нормированным отклонением результата наблюдения
с максимальным маловероятным нормированным отклонением результата наблюдения 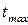 , которое могло бы иметь место при данном распределении и числе наблюдений
, которое могло бы иметь место при данном распределении и числе наблюдений 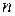 . Малая вероятность такого отклонения задается уровнем значимости
. Малая вероятность такого отклонения задается уровнем значимости 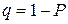 , определяющим вероятность нахождения случайной величины между
, определяющим вероятность нахождения случайной величины между 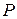 %-ным квантилем и
%-ным квантилем и 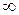 . Значение
. Значение 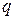 обычно выбирают от 1 до 10%. Значения
обычно выбирают от 1 до 10%. Значения 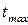 для нормального распределения при заданных
для нормального распределения при заданных 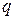 и
и 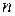 приведены в таблице 3
приведены в таблице 3
Таблица 3
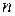
| 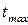
| |||
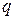 = 10% = 10%
| 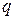 = 5% = 5%
| 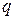 = 2,5% = 2,5%
| 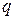 = 1% = 1%
| |
| 1,731 2,146 2,326 2,447 2,537 | 1,869 2,294 2,493 2,623 2,717 | 1,917 2,414 2,638 2,778 2,880 | 1,955 2,540 2,808 2,959 3,071 |
Если указанной отклонение проверяемого результата наблюдения оказывается больше 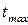 , его следует считать грубой погрешностью, которая, как и промах, должна быть исключена их полученной совокупности результатов наблюдения. После этого следует повторить их обработку с учетом меньшего числа
, его следует считать грубой погрешностью, которая, как и промах, должна быть исключена их полученной совокупности результатов наблюдения. После этого следует повторить их обработку с учетом меньшего числа 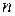 .
.
 2014-02-18
2014-02-18 800
800







