2014-02-18
330
Речь идет об определении критерия, при котором можно пренебречь меньшей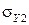 
из двух независимых составляющих общей погрешности, определяемой, согласно (12), как
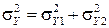(21)
Поскольку любые погрешности определяются приблизительно, их значение полагается представлять в виде числа, состоящего не более чем из двух значащих цифр. Иначе говоря, число, состоящее из большего количества значащих цифр, подлежит округлению до 2-х значащих цифр, поскольку остальные — недостоверны. Из этого условия следует, что если в (21)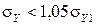 
, то после округления получим 
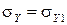, т. е. в этом случае следует пренебречь 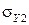. Итак, критерий ничтожности в исходном виде состоит в том, что, если вклад 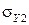в общую погрешность составляет меньше 0,05 (меньше 5%), то этой составляющей следует пренебречь.
Теперь найдем, во сколько раз при этом 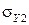должна быть меньше 
.
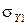Подставив (21) в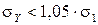 
, получим 
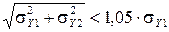. После возведения в квадрат, переноса 
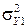в правую часть неравенства и извлечения корня получим 
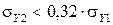или
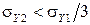(22)
Выражение (22) и есть критерий ничтожности, согласно которому независимой составляющей следует пренебрегать, если она меньше второй в 3 раза, т. е. составляет меньше 30%.
Этот критерий справедлив и для большего числа слагаемых, которые мы можем разбить на две группы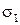 
и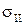 
с относительно большими (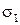) и малыми (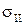) значениями:
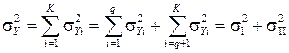(23)
Очевидно, что критерием в этом случае будет
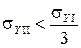(24)
